Metric Topology

The metric topology on a space $ X $ is generated by the basis consisting of open balls defined by a distance $ d $ on $ X $. This is also known as the distance-induced topology $ d $.

In a metric space $ (X, d) $, where $ d $ is a function that measures the distance between points in $ X $, I can define a metric topology made up of open sets constructed using "open balls."

An "open ball" centered at a point $ x \in X $ with a positive radius $ \varepsilon $ is the set of all points $ y $ in $ X $ that are less than $ \varepsilon $ units away from $ x $:

$$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$

In metric topology, a set is considered open if it can be expressed as a union of these open balls.

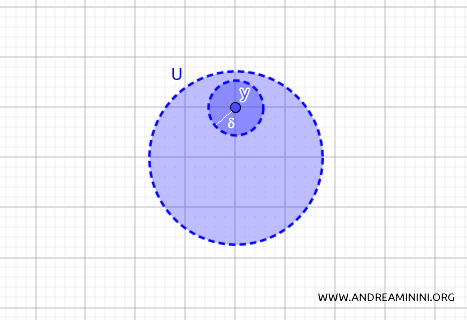
In other words, a set $ U \subset X $ is open in the metric topology induced by $ d $ if and only if, for every point $ y \in U $, there exists a radius $ \delta > 0 $ such that the ball $ B_d(y, \delta) $ is entirely contained within $ U $.

A Practical Example
Open Sets in Metric Topology
Types of Metrics
Additional Notes

A Practical Example

Let's consider the Euclidean space $\mathbb{R}$ in one dimension, which is essentially a line, equipped with the Euclidean distance.

The space $\mathbb{R}$ consists of all real numbers.

The distance $d$ between two points $x$ and $y$ on a line is defined as:

$$ d(x, y) = |x - y| $$

Here, $|x - y|$ denotes the absolute value of the difference between $x$ and $y$.

This distance fulfills all the properties of a metric.

Now, I can construct "open balls" in $\mathbb{R}$ using this distance.

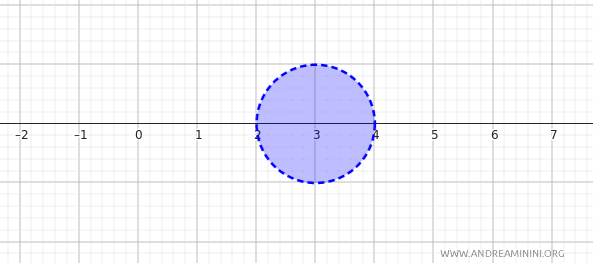
For instance, let’s take the point $x = 3$ and the radius $\varepsilon = 1$.

The open ball centered at $x = 3$ with a radius of $1$ is:

$$ B_d(3, 1) = \{y \in \mathbb{R} \mid d(3, y) < 1\} = \{y \in \mathbb{R} \mid |3 - y| < 1\} $$

By solving the inequality $ |3 - y| < 1 $, we find that $2 < y < 4$. Thus:

$$ B_d(3, 1) = (2, 4) $$

This indicates that the open ball centered at $3$ with a radius of $1$ corresponds to the open interval $(2, 4)$ on the real number line.

example

Sets such as $ (2, 4) $, $ (5, 7) $, or any open interval $(a, b)$ in $\mathbb{R}$ can be viewed as open balls or unions of open balls with respect to the distance $d(x, y) = |x - y|$.

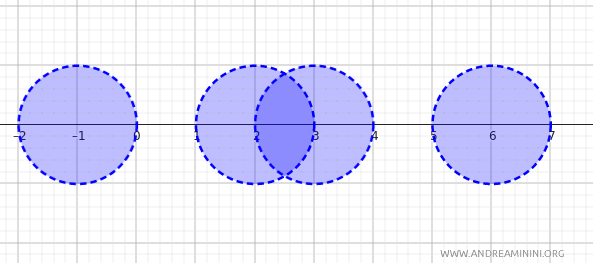
open sets

These intervals form a basis for the metric topology of $\mathbb{R}$.

Note. In the metric topology of $\mathbb{R}$, a set is open if, for every point within it, one can find an open interval (an open ball) that lies entirely within the set. For example, $(0, 5)$ is an open set because for every point in $(0, 5)$, I can find a small interval around that point that remains contained within $(0, 5)$.

In summary, by utilizing the distance $d(x, y) = |x - y|$ in $\mathbb{R}$, I arrive at the standard topology of open intervals, which I refer to as the metric topology on $\mathbb{R}$.

Open Sets in Metric Topology

In metric topology, a subset $ U \subset X $ is defined as an open set if, for every point $ y $ within $ U $, there exists an open ball centered at $ y $—essentially a “neighborhood” around $ y $ with a certain radius $\delta$—that lies entirely within $ U $.

At any point $ y $ within an open set $ U $, you can always find a small “circle” (or sphere, in higher dimensions) that remains completely contained within $ U $.

This characteristic defines the set as “open”: every point in $ U $ has a surrounding neighborhood that does not extend beyond $ U $.

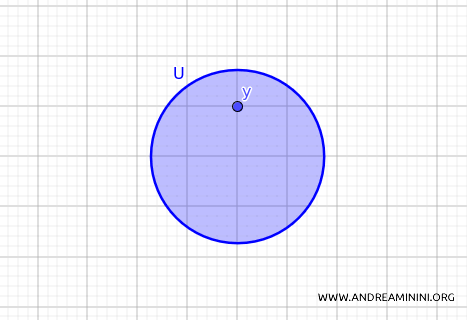
Here’s an example of an open set in a metric space $ \mathbb{R}^2 $.

example of an open set in metric topology

Closed sets, on the other hand, are the closures of open balls—sets that include both the boundary and every point $ y $ inside.

example of a closed set

In essence, this theorem captures the idea of openness through each point's “proximity” within the set.

Types of Metrics

Topologies induced by metrics can be based on various types, not only the standard Euclidean (circular) metric.

Some of the most commonly used metrics on the plane $ \mathbb{R}^2 $ include:

Standard metric (or Euclidean metric)
This metric forms open sets with a circular shape, known as open balls on the plane. It establishes the standard topology on $ \mathbb{R}^2 $. $$ d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} $$
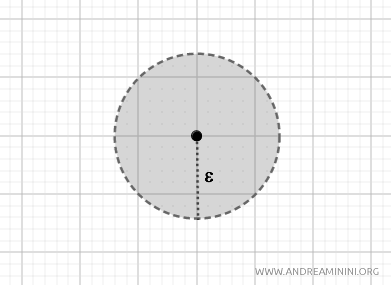
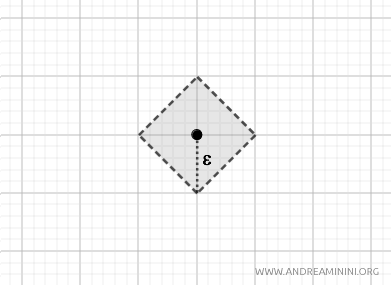
Taxi metric (or Manhattan distance)
Here, open balls have a diamond shape centered at $ p $. This metric also produces the standard topology on $ \mathbb{R}^2 $. $$ d_T(p, q) = |p_1 - q_1| + |p_2 - q_2|. $$
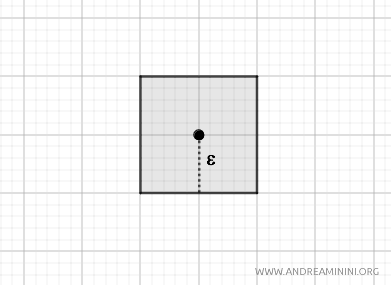
Max metric
With this metric, open balls are square-shaped and centered at $ p $, with side length $ 2\varepsilon $. It also generates a topology on $ \mathbb{R}^2 $.
$$ d_M(p, q) = \max\{|p_1 - q_1|, |p_2 - q_2|\} $$

Though these three metrics define open balls in distinct shapes (circular, diamond, and square), they all lead to a metric topology on $ \mathbb{R}^2 $.

Additional Notes

Some further insights into topologies induced by metrics.

Theorem: Comparison of Metric Topologies
Consider $d$ and $d'$ as two metrics defined on a set $X$, inducing the topologies $\mathcal{T}$ and $\mathcal{T}'$, respectively. The topology $\mathcal{T}'$ is finer than $\mathcal{T}$ if and only if, for every $x \in X$ and any $\varepsilon > 0$, there exists a $\delta > 0$ such that: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ where $B_{d}(x, \varepsilon)$ and $B_{d'}(x, \delta)$ denote the open balls centered at $x$ in the two metrics.
Simply put, $\mathcal{T}'$ is finer than $\mathcal{T}$ if every open set in the topology induced by $d$ contains at least one open set from the topology induced by $d'$.
Bounded Metric Theorem
In a metric space $ (X, d) $, a new bounded metric $ d'(x, y) = \min(d(x, y), \varepsilon) $, where $\varepsilon > 0$, can be defined. This metric preserves the same topology as $ d $, ensuring that the open sets generated by $ d $ and $ d' $ are identical.

And so forth.