Bounded Metric Theorem

In a metric space $ (X, d) $, it is possible to define a new bounded metric $ d'(x, y) = \min(d(x, y), 1) $, which generates the same topology as $ d $. This means the open sets defined by $ d $ and $ d' $ are identical.

In simpler terms, the new metric $ d'(x, y) $ is derived from the original metric $ d(x, y) $ in the metric space $ (X, d) $, where:

$$ d'(x, y) = \min(d(x, y), 1) $$

The metric $ d'(x, y) $ takes the value of $ d(x, y) $ unless it exceeds 1, making $ d' $ bounded since it can never be greater than 1.

The topology induced by $ d' $ is identical to that induced by $ d $.

This implies that the open sets defined by $ d' $ are exactly the same as those defined by $ d $. As a result, the "shape" of the open sets in the space does not change, even though $ d' $ is a bounded metric.

Note: Generally, $1$ can be replaced with any value $\varepsilon > 0$. $$ d'(x, y) = \min(d(x, y), \varepsilon) $$ In this case, distances would be capped at $\varepsilon$, while the induced metrics would still produce the same topology. For simplicity, I’ll illustrate this with the limit set to $ \varepsilon = 1 $.

A Practical Example
The Proof

A Practical Example

Consider the space $ \mathbb{R} $ with the standard metric:

$$ d(x, y) = |x - y| $$

Now, let’s define a new bounded metric:

$$ d'(x, y) = \min(|x - y|, 1) $$

In this new metric, distances are capped at 1.

For instance, if $ x = 2 $ and $ y = 5 $, the distance using the original metric is $ d(2, 5) = |2 - 5| = 3 $, but with the new bounded metric, it becomes $ d'(2, 5) = \min(3, 1) = 1 $. On the other hand, if $ x = 2 $ and $ y = 2.5 $, then $ d'(2, 2.5) = \min(|2 - 2.5|, 1) = 0.5 $, which matches the original metric since $ |2 - 2.5| < 1 $. In this case, the two metrics yield the same distance: $ d = d' = 0.5 $. $$ \begin{array}{|c|c|c|c|} \hline x & y & d & d' \\ \hline 2 & 5 & 3 & 1 \\ \hline 2 & 2.5 & 0.5 & 0.5 \\ \hline 6 & 8 & 2 & 1 \\ \hline \end{array} $$

The new metric $ d' $ "truncates" distances greater than 1, but the notions of proximity and open sets remain unchanged. Hence, the topology induced by $ d $ and $ d' $ is equivalent.

Why Does the Topology Remain the Same?

Open sets in a topology are defined as unions of open balls.

Although the open balls in $ d' $ may be smaller than those in $ d $, multiple $ d' $-balls can be combined to cover any open set defined by $ d $.

For example, consider the open ball $ B_d(3, 2) $ centered at $ 3 $ with a radius of $ 2 $.

This open ball consists of all points $ y \in \mathbb{R} $ such that the distance from $ x $ to $ y $ is less than $ r = 2 $, i.e.,

$$ B_d(x, r) = \{y \in \mathbb{R} \mid d(x, y) < r\} $$

In this case, $ x = 3 $ and $ r = 2 $.

$$ B_d(3, 2) = \{y \in \mathbb{R} \mid d(3, y) < 2\} $$

Using the standard metric ($ d(x, y) = |x - y| $), the open ball $ B_d(3, 2) $ contains all real numbers $ y $ satisfying:

$$ |3 - y| < 2 $$

Rewriting this condition:

$$ -2 < 3 - y < 2 $$

$$ -5 < -y < -1 $$

$$ 1 < y < 5 $$

Thus, $ B_d(3, 2) $ corresponds to the open interval $ (1, 5) $, which includes all points within 2 units of 3 on the real line.

$$ B_d(3, 2) = (1, 5) $$

Here is a visual representation on the number line:

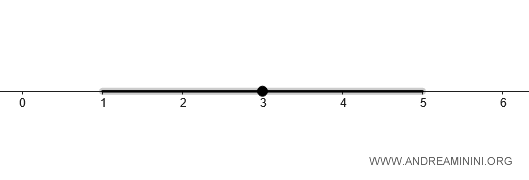
example

To cover the interval $ (1, 5) $ using $ d' $, we can use the union of smaller balls, such as:

$$ B_{d'}(2, 1) \cup B_{d'}(3, 1) $$

The first ball covers $ (1, 3) $, and the second covers $ (3, 5) $. Together, they fully cover the interval $ (1, 5) $.

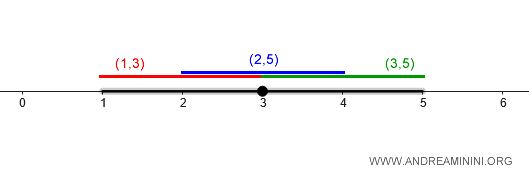
example

This demonstrates that $ d' $ and $ d $ produce the same open sets, ensuring the topology remains unchanged.

The Proof

To prove that $ d' $ induces the same topology as $ d $, we first verify that $ d' $ is a valid metric, satisfying the following properties:

$ d'(x, y) \geq 0 $,
$ d'(x, y) = 0 $ if and only if $ x = y $,
$ d'(x, y) = d'(y, x) $,
$ d' $ satisfies the triangle inequality.

The triangle inequality holds because:

When $ d(x, y) $ or $ d(y, z) $ are greater than or equal to 1, $ d'(x, y) + d'(y, z) \geq d'(x, z) $ is straightforward since $ d'(x, y) + d'(y, z) = 1 + 1 = 2 $, and $ d'(x, z) \leq 1 $.
When $ d(x, y) < 1 $ and $ d(y, z) < 1 $, we have $ d'(x, y) = d(x, y) $, $ d'(y, z) = d(y, z) $, and $ d'(x, z) = d(x, z) $. Since $ d $ is a metric by assumption, the triangle inequality holds for $ d' $ as well.

Next, we demonstrate that the topologies $ T $ (induced by $ d $) and $ T' $ (induced by $ d' $) are identical by showing:

$ T $ is finer than $ T' $,
$ T' $ is finer than $ T $.

A] $ T $ is finer than $ T' $

The original topology $ T $ is finer because:

When the radius $ r $ of the ball is less than or equal to 1, the open balls are identical: $$ B_d(x, r) = B_{d'}(x, r) $$
For $ r > 1 $, the open ball in $ T $ contains the corresponding ball in $ T' $: $$ B_d(x, r) \supseteq B_{d'}(x, r) $$

B] $ T' $ is finer than $ T $

The reverse also holds because:

When $ r \leq 1 $, the open balls are the same: $$ B_d(x, r) = B_{d'}(x, r) $$
For $ r > 1 $, unions of smaller $ d' $-balls can cover any open set in $ T $.

Conclusion

Since $ T $ is finer than $ T' $ and $ T' $ is finer than $ T $, we conclude $ T = T' $, proving the two topologies are identical.