Metric Equivalence

Two metric spaces are considered equivalent if there exists a function $f : X \to Y$ that satisfies the following conditions:

Bijective: every element in $X$ corresponds to one and only one element in $Y$, and vice versa.
Distance-preserving: for any points $x_1, x_2 \in X$, the distance between $x_1$ and $x_2$ in $X$ is exactly the same as the distance between their images $f(x_1)$ and $f(x_2)$ in $Y$. Formally: $$ d_X(x_1, x_2) = d_Y(f(x_1), f(x_2)) $$

If such a function exists, the spaces $X$ and $Y$ are said to be isometric, meaning they are equivalent.

In essence, metric equivalence involves comparing two metric spaces ($X, d_X$ and $Y, d_Y$) to determine whether they are "essentially the same" in terms of how distances are measured.

If two metric spaces are isometric, they share the same topology. In other words, their open sets (or the "general shape" of the space) are identical. However, the reverse is not always true.
Having the same topology does not necessarily mean two spaces are isometric (or equivalent), as isometry is a stronger condition than topological equivalence. Isometry requires that distances are preserved exactly, not just the structure of open sets.

A Practical Example

Consider two metric spaces:

$X = \{a, b, c\}$ with the metric $d_X$ defined as: $$ d_X(a, b) = 1, \quad d_X(b, c) = 2, \quad d_X(a, c) = 3 $$
$Y = \{p, q, r\}$ with the metric $d_Y$ defined as: $$ d_Y(p, q) = 1, \quad d_Y(q, r) = 2, \quad d_Y(p, r) = 3 $$

Now, define a function $f : X \to Y$ as follows:

$$ f(a) = p, \quad f(b) = q, \quad f(c) = r $$

Let’s check if it preserves distances:

$d_X(a, b) = 1$, and $d_Y(f(a), f(b)) = d_Y(p, q) = 1$
$d_X(b, c) = 2$, and $d_Y(f(b), f(c)) = d_Y(q, r) = 2$
$d_X(a, c) = 3$, and $d_Y(f(a), f(c)) = d_Y(p, r) = 3$

Since all distances are preserved, $f$ is an isometry, which means the metric spaces $X$ and $Y$ are isometric, or equivalent.

Example 2

On the plane, the taxicab metric ($d_T$) and the standard metric ($d$) induce the same topology. This means they share the same concept of open sets.

Let’s determine whether these two metric spaces are also isometric.

Under the taxicab metric ($d_T$), the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is defined as:

$$ d_T((x_1, y_1), (x_2, y_2)) = |x_1 - x_2| + |y_1 - y_2| $$

This metric measures distance as though you were navigating a grid, following horizontal and vertical paths (like a taxi moving through a city grid).

In contrast, the standard metric ($d$) measures the straight-line distance between two points using the Euclidean formula:

$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$

To check for isometry, assume there exists a function $f : \mathbb{R}^2 \to \mathbb{R}^2$ that preserves distances under both metrics. Consider two points: $ A = (1, 1) $ and $ B = (2, 2) $.

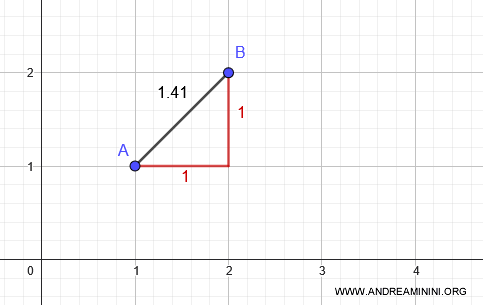
example

Under the taxicab metric, the distance between these points is:

$$ d_T((2, 2), (1, 1)) = |2 - 1| + |2 - 1| = 2 $$

Under the standard metric, the distance is approximately 1.41:

$$ d((1, 1), (2, 2)) = \sqrt{(1 - 2)^2 + (1 - 2)^2} = \sqrt{2} \approx 1.41 $$

Since the distances differ, it’s impossible to construct an isometry that preserves distances between these two metric spaces. Therefore, the plane with the taxicab metric is not isometric to the plane with the standard metric.

In conclusion, while the taxicab metric ($d_T$) and the standard metric ($d$) induce the same topology (i.e., they share the same concept of open sets), they are not isometric.

And so on.