Levenshtein Distance

This metric is especially useful in applications like spell checkers, where it helps to compare similar words and suggest corrections. It’s commonly applied to measure string similarity.

To calculate the Levenshtein distance, I build a matrix in which each cell represents the minimum cost of transforming one substring into another, moving cell by cell to accumulate the least number of operations.

Unlike the Hamming distance, Levenshtein distance also applies to strings of different lengths.

A Practical Example

Consider the strings \( s \) and \( t \):

$$ s = "kitten" $$

$$ t = "sitting" $$

I want to determine the Levenshtein distance between these two words—that is, the minimum number of edits (insertions, deletions, or replacements) required to turn "kitten" into "sitting".

1. Replacement
   Replace \( k \) with \( s \): $$ "kitten" \rightarrow "sitten" $$
2. Replacement
   Replace \( e \) with \( i \): $$ "sitten" \rightarrow "sittin" $$
3. Insertion
   Add a \( g \) at the end: $$ "sittin" \rightarrow "sitting" $$

In total, I performed 3 operations (2 replacements and 1 insertion), so the Levenshtein distance between "kitten" and "sitting" is 3.

To represent this process, I can create a matrix with dimensions \( (m+1) \times (n+1) \), where \( m \) is the length of "kitten" (6) and \( n \) is the length of "sitting" (7).

Extra rows and columns are included to handle transformations from and to an empty string.

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1
i	2
t	3
t	4
e	5
n	6

The cell \( (0, j) \) shows the cost to transform an empty string into the substring of "sitting" up to \( j \), so the cost increases from 0 to 7.

The cell \( (i, 0) \) shows the cost to transform the substring of "kitten" up to \( i \) into an empty string, so the cost increases from 0 to 6.

For each cell \( (i, j) \), I calculate the minimum cost by considering:

1. Deleting a character from "kitten" (cost of the cell above, \( +1 \))
2. Inserting a character into "kitten" (cost of the cell to the left, \( +1 \))
3. Replacing a character (cost of the diagonal cell) if characters are different (otherwise, no additional cost).

I proceed to fill in the matrix step by step:

	""	s	i	t	t	i	n	g
""	0	1	2	3	4	5	6	7
k	1	1	2	3	4	5	6	7
i	2	2	1	2	3	4	5	6
t	3	3	2	1	2	3	4	5
t	4	4	3	2	1	2	3	4
e	5	5	4	3	2	2	3	4
n	6	6	5	4	3	3	2	3

For example, transforming an empty string into "s", "si", "sit", and so on, adds a cost of 1 for each column.

To transform "k", "ki", "kit", and so on into an empty string, the cost increases by 1 for each row.

• The cell (1,1) shows the cost of changing "k" into "s", which is 1 since only one substitution is required (k→s).
  
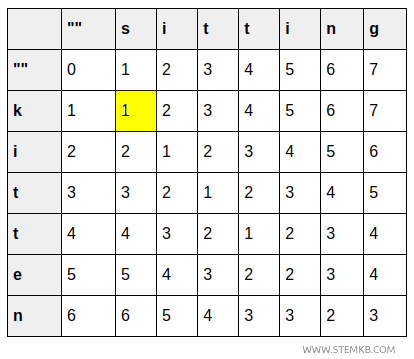
• The cell (2,2) shows the cost of transforming "ki" into "si", which remains 1 because the second letter is the same (i).
• The cell (3,3) shows the cost of changing "kit" into "sit", which is still 1 since the third letter matches (t).
• The cell (4,4) shows the cost of transforming "kitt" into "sitt", which is also 1 as the fourth letter matches (t).
• The cell (5,5) shows the cost of turning "kitte" into "sitti", which is 2 due to one substitution (e→i).
  
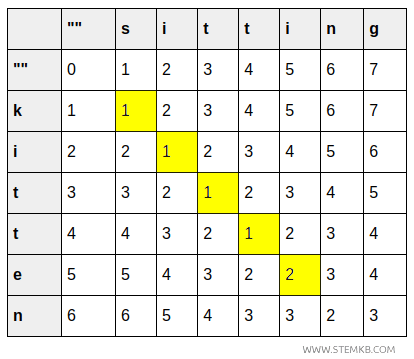
• The cell (6,6) shows the cost of changing "kitten" to "sittin", which remains 2 because the sixth letter is the same (n).
• The cell (6,7) shows the cost of converting "kitten" to "sitting", which becomes 3 as an additional letter (g) must be added.
  

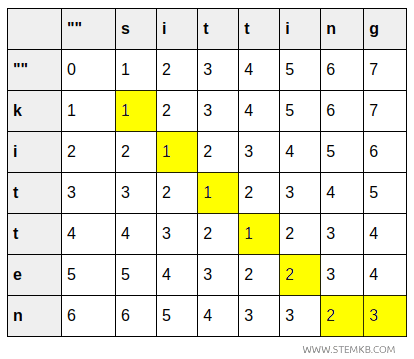
In this way, I reach the final cell, which holds the overall cost.

The bottom-right cell \( (6,7) \) contains the minimum cost of transforming "kitten" into "sitting", which is 3.

This value corresponds to the Levenshtein distance, as I found earlier: it requires 1 substitution (`k → s`), 1 substitution (`e → i`), and 1 insertion (`g`).

Topology Induced by Levenshtein Distance

The Levenshtein distance defines a metric space on strings, similar to the Hamming distance, as it meets the fundamental properties of a metric.

1. Non-negativity: The Levenshtein distance between two strings \( x \) and \( y \) is always zero or greater, and \( D_L(x, y) = 0 \) only if \( x = y \). This implies no operations are needed to transform a string into itself, so the distance is zero only for identical strings.
2. Symmetry: The Levenshtein distance is symmetric, meaning \( D_L(x, y) = D_L(y, x) \). The number of operations needed to transform \( x \) into \( y \) is the same as transforming \( y \) into \( x \), as the operations (insertion, deletion, and replacement) apply in both directions.
3. Triangle Inequality: The Levenshtein distance satisfies the triangle inequality, that is, \( D_L(x, z) \leq D_L(x, y) + D_L(y, z) \). In other words, the direct distance between \( x \) and \( z \) cannot exceed the distance found by going through a third string \( y \). This occurs because each step required to transform \( x \) into \( z \) can be broken down into steps from \( x \) to \( y \) and from \( y \) to \( z \).

Thanks to these properties, the Levenshtein distance generates a metric space on strings.

Since it satisfies the axioms of a metric space, I can also use it to define an induced metric topology on strings.

Given a radius \( r \) and a string \( x \), I can construct an open ball centered at \( x \) as the set of all strings \( y \) whose Levenshtein distance from \( x \) is less than \( r \):

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$

The union of open balls \( B(x, r) \) defines the open sets of this topology.

This framework has important applications, especially in fields where "proximity" between strings is valuable. For instance, in automatic spelling correction, a word that has a small Levenshtein distance from another dictionary word might be suggested as a correction.

Therefore, the Levenshtein distance lets me treat strings as elements of a metric space and leverage the induced metric topology to analyze their proximity.

A Practical Example

Consider a set \( X \) of three-character strings:

$$ X = \{"cat", "bat", "cut"\} $$

I define a basis for the topology by considering open balls with radius \( r = 2 \) centered on each string in \( X \).

$$ B(x, r) = \{ y \mid D_L(x, y) < r \} $$ 

Each open ball with radius \( r = 2 \) includes all strings that differ by exactly 1 character from the center string, according to Levenshtein distance.

Note: Using a radius \( r = 2 \) implies including strings that differ by at most one position from the center string, as the concept of an "open set" excludes the boundary. Thus, for an open set with radius \( r = 2 \), the relationship is "strictly less than 2": $$ B(x, 2) = \{ y \mid D_L(x, y) < 2 \} $$ To define "closed sets" that include the boundary, I would use "less than or equal to 2," including all strings within a maximum distance of 2 edits from the center string: $$ C(x, 2) = \{ y \mid D_L(x, y) \le 2 \} $$

I check the open balls of radius \( 2 \) for each string in \( X \):

1. Open ball centered on "cat" $$ B("cat", 2) = \{"cat", "bat"\} $$ These strings require at most one character substitution to transform "cat" into "bat", "rat", or "mat".
2. Open ball centered on "bat" $$ B("bat", 2) = \{"bat", "cat"\} $$ This open ball includes all strings that can be transformed into "bat" with at most one edit.
3. Open ball centered on "cut" $$ B("cut", 2) = \{"cut"\} $$ In this case, none of the strings in set \( X \) can be transformed into "cut" with just one edit. Only "cut" itself belongs to this set as it can be transformed into itself with zero edits.

The sets \( B("cat", 2) \), \( B("bat", 2) \), and \( B("cut", 2) \) form a basis for the topology induced by the Levenshtein distance with radius \( r = 1 \).

With this basis, I can derive all other open sets as arbitrary unions of these open balls of radius \( 2 \).

For example, the union of \( B("bat", 1) \) and \( B("cut", 1) \)

$$ B("bat", 1) \cup B("cut", 1) $$

Knowing that \( B("cat", 2) = \{"cat", "bat"\} \) and \( B("cut", 2) = \{"cut"\} \)

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat"\} \cup \{"cut"\} $$

$$ B("bat", 1) \cup B("cut", 1) = \{"cat", "bat", "cut"\} $$

The set \( \{"cat", "bat", "cut"\} \) is another open set in this topology.

Through this construction, I have a metric topology on \( X \) induced by Levenshtein distance, and I can generate any open set as a union of these basic elements.

And so on.