Theorem Comparing Topologies Induced by Metrics

Let $d$ and $d'$ be two metrics on a set $X$, and let $\mathcal{T}$ and $\mathcal{T}'$ denote the topologies induced by $d$ and $d'$, respectively. The topology $\mathcal{T}'$ is finer than $\mathcal{T}$ if and only if, for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$ where $B_{d}(x, \varepsilon)$ and $B_{d'}(x, \delta)$ represent open balls centered at $x$ with radii $\varepsilon$ and $\delta$, respectively, in the metrics $d$ and $d'$.

To put it simply, if we consider two different ways ($d$ and $d'$) of measuring distances on a set $X$, each metric generates an associated topology—a collection of open sets.

The topology $\mathcal{T}$, induced by $d$
The topology $\mathcal{T}'$, induced by $d'$

The theorem states that $\mathcal{T}'$ is finer than $\mathcal{T}$ (meaning $\mathcal{T}'$ includes more open sets) if and only if every open set in the topology induced by $d$ contains at least one open set from the topology induced by $d'$.

This perspective makes the relationship between the two topologies clearer and highlights the connection between metrics and open sets.

A Practical Example
The Proof

A Practical Example

Let’s consider the set $X = \mathbb{R}^2$, the Cartesian plane, with two different metrics:

Euclidean Metric: $d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$. The open balls in this metric are circles: $$ B_d((x, y), \varepsilon) = \{(u, v) \in \mathbb{R}^2 : \sqrt{(u - x)^2 + (v - y)^2} < \varepsilon\} $$
Discrete Metric: $d'((x_1, y_1), (x_2, y_2)) = \begin{cases} 0 & \text{if } (x_1, y_1) = (x_2, y_2), \\ 1 & \text{if } (x_1, y_1) \neq (x_2, y_2) \end{cases}$. The open balls in this metric are defined as follows: \[ B_{d'}((x, y), \delta) = \begin{cases} \{(x, y)\} & \text{if } \delta \leq 1, \\ X & \text{if } \delta > 1. \end{cases} \]

We aim to show that the discrete topology is finer than the Euclidean topology.

According to the theorem:

$$ \mathcal{T}' \text{ is finer than } \mathcal{T} \iff \forall x \in X, \forall \varepsilon > 0, \ \exists \ \delta > 0 \text{ such that } B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

Take a generic point $P = (x_0, y_0) \in \mathbb{R}^2$ and select a radius $\varepsilon > 0$ for the ball $B_d(P, \varepsilon)$ in the Euclidean topology.

The ball $B_d(P, \varepsilon)$ is a circle centered at $P = (x_0, y_0)$ with radius $\varepsilon$.

Now, consider an open ball $B_{d'}(P, \delta)$ in the discrete metric. By definition, such a ball is:

$\{P\}$ if $\delta \leq 1$,
$X$ (the entire space) if $\delta > 1$.

In the discrete topology, every single point is an open set.

Let $\delta = 1$. In this case, $B_{d'}(P, \delta) = \{P\}$, which is clearly contained within $B_d(P, \varepsilon)$, since $P \in B_d(P, \varepsilon)$.

Thus, for every $P = (x_0, y_0)$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that:

$$ B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon) $$

For example, consider the point $P = (1, 2) \in \mathbb{R}^2$. In the Euclidean topology, an open ball centered at $P$ with any radius (e.g., $\varepsilon = 0.4$) is an open set.
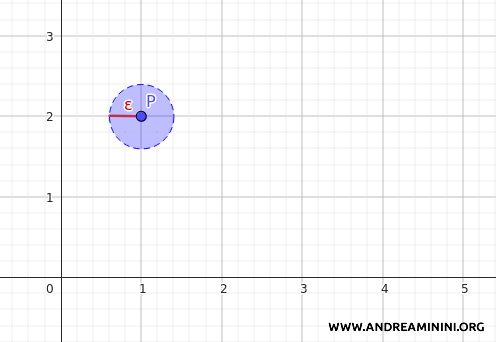
example
In the discrete topology, any individual point is an open set. Therefore, $\{P\} = \{(1, 2)\}$ is also an open set in the discrete topology. Notice that $\{P\} \subseteq B_d(P, \varepsilon)$, as $P$ lies within the circle $B_d(P, \varepsilon)$. This reasoning applies to any other point in the plane, confirming that every open set in the Euclidean topology (such as $B_d(P, \varepsilon)$) contains at least one open set from the discrete topology (like $\{P\}$).

In conclusion, we have verified that the conditions of the theorem are met: the discrete topology ($\mathcal{T}'$) is finer than the Euclidean topology ($\mathcal{T}$) because, for every point $P$ and every radius $\varepsilon > 0$, there exists a $\delta > 0$ (in this case, $\delta = 1$) such that $B_{d'}(P, \delta) \subseteq B_d(P, \varepsilon)$.

The Proof

The proof involves demonstrating the theorem in both directions:

If $\mathcal{T}'$ is finer than $\mathcal{T}$, then for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.
If for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$, then $\mathcal{T}'$ is finer than $\mathcal{T}$.

The proof can be divided into two parts:

A] Part 1

If the topology $\mathcal{T}'$ is finer than $\mathcal{T}$, then for every $x \in X$ and $\varepsilon > 0$, there exists a $\delta > 0$ such that $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$.

By definition, if $\mathcal{T}'$ is finer than $\mathcal{T}$, then every open set in $\mathcal{T}$ is also open in $\mathcal{T}'$. This implies that every open ball $B_d(x, \varepsilon)$ (which is open in $\mathcal{T}$) is also open in $\mathcal{T}'$.
Since $B_d(x, \varepsilon)$ is open in $\mathcal{T}'$, by the definition of openness , every point $x$ in $B_d(x, \varepsilon)$ has a neighborhood $B_{d'}(x, \delta)$ (open in the metric $d'$) that is entirely contained within $B_d(x, \varepsilon)$.
Thus, for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$

B] Part 2

Conversely, if for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$, then $\mathcal{T}'$ is finer than $\mathcal{T}$.

By assumption, for every $x \in X$ and every $\varepsilon > 0$, there exists a $\delta > 0$ such that: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$
Consider any open set $U$ in the topology $\mathcal{T}$. By definition, $U$ is the union of open balls $B_d(x, \varepsilon)$. We aim to show that $U$ is also open in $\mathcal{T}'$.
Take any point $x \in U$. Since $U$ is open in $\mathcal{T}$, there exists an open ball $B_d(x, \varepsilon) \subseteq U$.
Thus, we can find an open ball $B_{d'}(x, \delta)$ such that: $$ B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon) $$
Since $B_{d'}(x, \delta) \subseteq B_d(x, \varepsilon)$, it follows that $B_{d'}(x, \delta) \subseteq U$. Therefore, $U$ is also open in the topology $\mathcal{T}'$.

This completes the proof in both directions.

And so on.