Disjoint Sets

Two sets A and B are called disjoint sets when they share no elements in common.

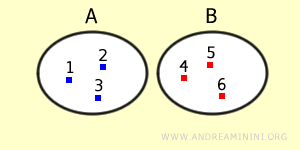
When two sets are disjoint, their intersection is equal to the empty set. $$ A ⋂ B = Ø $$

A Practical Example

Set A consists of even numbers while set B is made up of odd numbers.

$$ A = \{ 2 \ , \ 4 \ , \ 6 \ , \ 8 \} $$

$$ B = \{ 1 \ , \ 3 \ , \ 5 \ , \ 9 \} $$

Sets A and B do not share any common elements.

In a graphical representation using Euler-Venn diagrams, the two sets do not overlap.

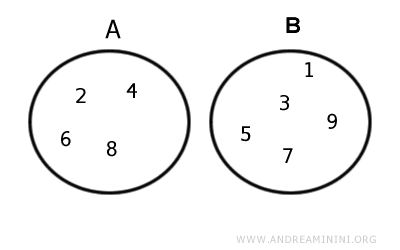
Their intersection is equal to the empty set.

$$ A ⋂ B = Ø $$

Therefore, sets A and B are disjoint sets.

And so on.