Intersection of Sets
The intersection of two sets A and B is the set containing all the elements that belong to both set A and set B.
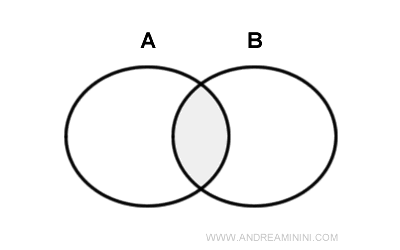
The symbol for intersection is ⋂.
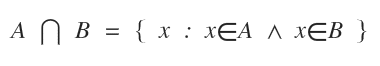
This notation is read as "the intersection of A and B" or "A intersected with B".
Intersection of Multiple Sets. When intersecting more than two sets, this more concise notation can be used to indicate the intersection $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$
When two sets have no elements in common, the intersection A⋂B is an empty set.
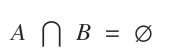
In this case, the two sets are called disjoint sets.
A Practical Example
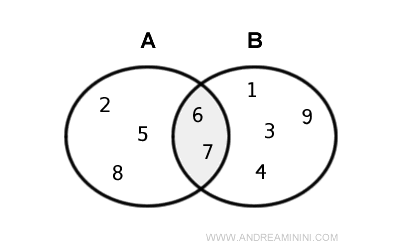
Consider two finite sets A and B
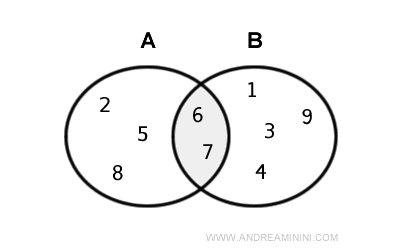
$$ A = \{ 2,5,6,7, 8 \} $$
$$ B = \{ 1,3,4,6, 7,9 \} $$
The two sets have two elements in common.
$$ A = \{ 2,5, \color{red}6,\color{red}7, 8 \} $$
$$ B = \{ 1,3,4,\color{red}6, \color{red}7,9 \} $$
Therefore, the intersection between the two sets A⋂B consists of two elements (6,7).
$$ A \cap B = \{ 6,7 \} $$
Here is the representation of the intersection with Euler-Venn diagrams
Types of Intersection
The intersection between two sets A and B can result in different outcomes
- The intersection A⋂B is a proper subset of both sets.
Example. Given two sets $$ A = \{ 2,5,6,7, 8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ Their intersection is $$ A \cap B = \{ 6,7 \} $$ In this case, the intersection is a proper subset of both A and B $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$ This is the example already discussed
- The intersection A⋂B is a proper subset of one of the sets and an improper subset of the other set. This occurs if one of the sets is a proper subset of the other, for example, A⊂B.
Example. Given two sets $$ A = \{ 3,6,7 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ Their intersection is $$ A \cap B = \{ 3, 6,7 \} $$ Visually
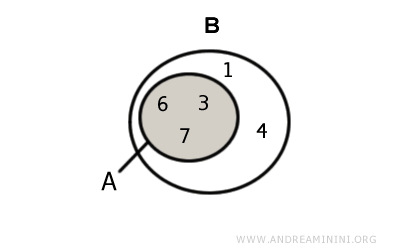
In this case, the intersection is an improper subset of A because it coincides with A $$ A \cap B = A $$ and a proper subset of B because there is at least one element in B that does not belong to A $$ A \cap B ⊂ B $$ - The intersection A⋂B is an improper subset of both sets. This happens in two different situations.
A] When the sets are disjoint sets, the intersection is an empty set which, by definition, is an improper subset of every set.
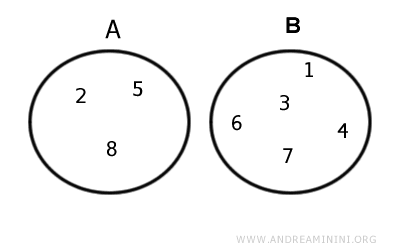
Example. Given two sets $$ A = \{ 2,5,8 \} $$ $$ B = \{ 1,3,4,6, 7,9 \} $$ Their intersection is an empty set $$ A \cap B = \{ \ \ \} = Ø $$ In this case, the two sets A and B have no elements in common.
B] When the sets are equal sets. In this case, the intersection is a set equal to both A and B
The empty set is an improper subset of all sets. Therefore, it is an improper subset of both A and B $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$
Example. Given two sets $$ A = \{ 1,2,3,4 \} $$ $$ B = \{ 1,2,3,4 \} $$ Their intersection is a set equal to both A and B $$ A \cap B = A = B $$ In this case, the two sets A and B have all elements in common. They are equal sets.
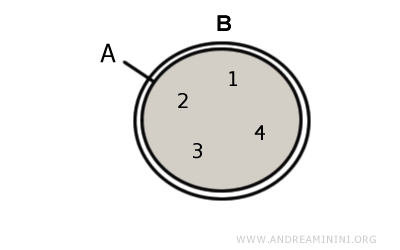
When two sets are equal, they are improper subsets of each other
Properties of Intersection
The intersection of two sets adheres to properties similar to those of addition and multiplication of numbers.
- Commutative Property
Switching the order of the sets does not change the intersection $$ A \cap B = B \cap A $$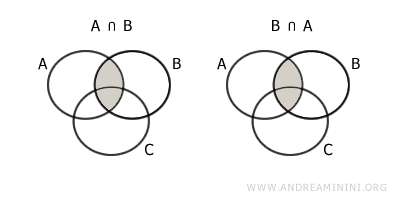
- Associative Property
The intersection of A⋂B with C is the same as the intersection of A with B⋂C. $$ (A \cap B) \cap C = A \cap (B \cap C) $$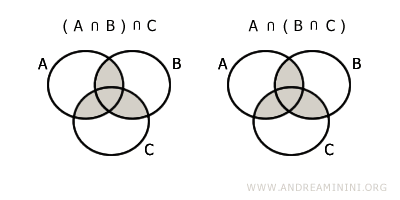
- Distributive Property with Respect to Union
The intersection of A with B∪C is the same as the union of the intersections A⋂B and A⋂C
$$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$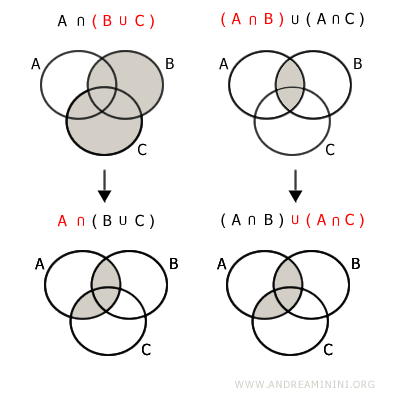
And so on.
