Bounded Sets
What Is a Bounded Set?
A set is considered bounded if there exists a real number M such that every element in the set lies between -M and +M. In other words, $$ -M \leq a \leq +M \quad \forall \: a \in A $$ or equivalently, $$ |a| \leq M \quad \forall \: a \in A $$
If a set is bounded, it is both bounded above and bounded below.
Proof
A] Starting with the inequality:
$$ |a| \leq M \quad \forall \: a \in A $$
By the definition of absolute value, this implies:
$$ -M \leq a \leq M \quad \forall \: a \in A $$
Thus, we can take -M as a lower bound and +M as an upper bound.
B] Now, suppose we start with the inequality:
$$ l \leq a \leq L \quad \forall \: a \in A $$
where \( l \) and \( L \) are real numbers. To establish a bound, we take:
$$ M = \max(|l|, |L|) $$
This allows us to write:
$$ |a| \leq M \quad \forall \: a \in A $$
which in turn satisfies:
$$ -M \leq l \leq a \leq L \leq M \quad \forall \: a \in A $$
A Practical Example
Consider the real set \( A \) containing seven elements:
$$ A = \{ -7, 4, 2, 6, 3, 5, 1 \} $$
The set has infinitely many lower bounds in the interval (-∞, -7] and infinitely many upper bounds in the interval [6, +∞).
To find the tightest bounds, we identify the greatest lower bound \( l = -7 \) and the smallest upper bound \( L = 6 \).
$$ l = -7, \quad L = 6 $$
We then determine \( M \), the largest absolute value between \( l \) and \( L \):
$$ M = \max(|l|, |L|) $$
$$ M = \max( |-7|, |6|) $$
$$ M = \max(7, 6) $$
$$ M = 7 $$
Since there exists a real number \( M = 7 \) such that:
$$ -M \leq a \leq M \quad \forall a \in A $$
$$ -7 \leq a \leq 7 \quad \forall a \in A $$
the set \( A \) meets the boundedness condition, meaning it is a bounded set.
Lower-Bounded Sets
A set is said to be bounded below if there exists a real number \( M \) such that every element in the set is greater than or equal to \( M \): $$ a \geq M \quad \forall \: a \in A $$
A lower-bounded set always has at least one lower bound.
If a set is bounded below, it has a finite number known as its greatest lower bound or infimum.
In a non-empty, bounded set of real numbers, the greatest lower bound is the largest of all lower bounds.
$$ m = \inf(A) = \begin{cases} m \leq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists \: a \in A \text{ such that } m + \epsilon > a \end{cases} $$
Example: The set of positive real numbers \( R^+ \) is bounded below since all its elements lie in the interval (0, +∞). The set is bounded below by \( M = 0 \), which is the largest lower bound (infimum). However, it is unbounded above because it has no upper bound, meaning its supremum is +∞.
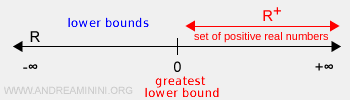
If a set is not bounded below, its infimum is negative infinity (-∞):
$$ \inf(A) = -\infty \Leftrightarrow \forall \: l \in R, \: \exists \: a \in A \text{ such that } a < l $$
Upper-Bounded Sets
A set is bounded above if there exists a real number \( M \) such that every element in the set is less than or equal to \( M \): $$ a \leq M \quad \forall \: a \in A $$
An upper-bounded set always has at least one upper bound.
If a set is bounded above, it has a finite number known as its least upper bound or supremum.
In a non-empty, bounded set of real numbers, the least upper bound is the smallest of all upper bounds.
$$ M = \sup(A) = \begin{cases} M \geq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists \: a \in A \text{ such that } M - \epsilon < a \end{cases} $$
Example: The set of negative real numbers \( R^- \) is bounded above because all its elements lie in the interval (-∞, 0). The set is bounded above by \( M = 0 \), which is the least upper bound (supremum). However, it is unbounded below because it has no lower bound, meaning its infimum is -∞.
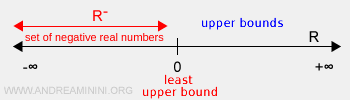
If a set is not bounded above, its supremum is positive infinity (+∞):
$$ \sup(A) = +\infty \Leftrightarrow \forall \: L \in R, \: \exists \: a \in A \text{ such that } a > L $$
Bounded Set in the Plane
A set \(A \subseteq \mathbb{R}^2\) is said to be bounded in the plane if there exists a positive real number \(M > 0\) and a point \(P_0\) in the plane such that, for every point \(P\) in \(A\), the distance between \(P\) and \(P_0\) is less than \(M\). \[ \exists \ P_0 \in \mathbb{R}^2, \exists \ M > 0 \text{ such that } \forall \ P \in A, \quad d(P, P_0) < M \] where \(d(P, P_0)\) denotes the Euclidean distance.
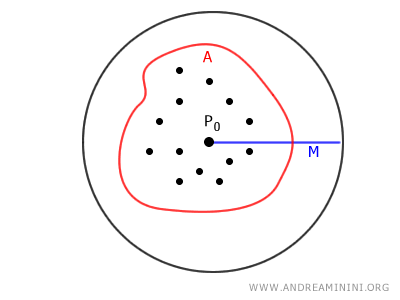
In other words, a set in \(\mathbb{R}^2\) is bounded if all its points lie within some circle of finite radius.
More generally, a set is bounded if it does not extend infinitely in any direction and can be entirely contained within a sufficiently large circle.
Examples of bounded sets in the plane include:
- A circle of radius \(r\), with or without its boundary.
- A square, a rectangle, a triangle, or any other polygon.
- Any closed figure with finite dimensions.
Note. Conversely, examples of unbounded sets include a straight line, a parabola, a spiral that grows without bound like \(y = x^2\), or an entire quadrant of the Cartesian plane.
And so on.
