Set Collections

A set collection is a set whose elements are sets themselves.

In other words, it's a set made up of other sets.

This concept is utilized across various branches of mathematics, including set theory, topology, and abstract algebra.

What's it good for? A set collection can be used to define more complex mathematical structures or to explore relationships between different sets.

Here are a few examples of set collections:

• Set family
  This is a collection of sets where the sets share some common property or meet certain criteria. For example, the family of all open sets in a topological space.
• Set partition
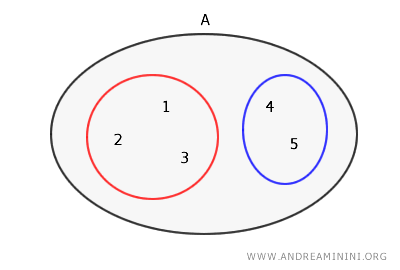
  A set partition is a collection of disjoint sets, such that the union of all these sets equals the original set in its entirety. Every element of the original set belongs to one of the sets in the partition.

  For instance, given a set A={1,2,3,4,5}, a partition of set A could be a collection including the subsets { {1,2,3} , {4,5} } as elements.
  

• Power set (set of all subsets)
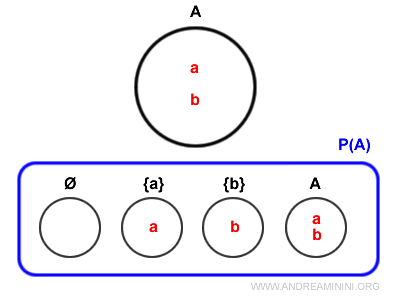
  It's a collection that includes all possible subsets of a given set, including the empty set and the set itself.

  For example, given a set A={a,b} consisting of two elements, the power set P(A) is a collection of four sets: { {}, {a}, {b}, {a,b} }
  

These concepts are fundamental for understanding and working with mathematical structures in greater detail and for exploring the relationships and properties of sets in various mathematical contexts.