Difference Between Sets

The difference between two sets A and B is a set (called the difference set) consisting of elements in set A that are not in set B. $$ A-B = \{ x \ | \ x \ \in A \ ∧ \ x \notin \ B \} $$ This is read as "A minus B". Here is the Venn diagram.

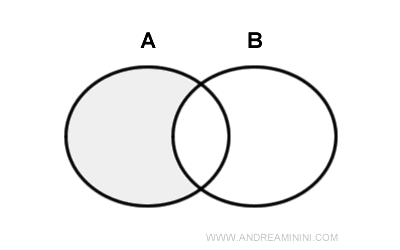
Sometimes the difference between sets is also denoted as follows

$$ A \text{ \ } B $$

This is read as "the set A\B is the complement of set B".

A Practical Example

Let's consider two finite sets A and B

$$ A = \{ 0, 2, 4, 8, 10 \} $$

$$ B = \{ 2, 4, 6, 12 \} $$

The difference between the two sets is a set A-B containing elements of A that are not in B

$$ A-B = A \text{ \ } B = \{ 0, 8, 10 \} $$

The difference set consists of elements in A not shared with B, namely { 0, 8, 10}.

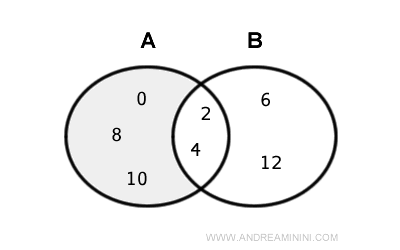
The common elements between the two sets, namely 2 and 4, are removed from the difference set.

Example 2

Let's consider two finite sets A and B

$$ A = \{ 1, 2, 3, 4, 5, 6, 7 \} $$

$$ B = \{ 2, 4, 6 \} $$

In this case, set B is a proper subset of set A.

The difference A-B is a set consisting of elements in A that are not in B

$$ A-B = A \text{ \ } B = \{ 1, 3, 5,7 \} $$

The difference set consists of elements { 1, 3, 5, 7}.

In the graphical representation using Euler-Venn diagrams, the difference set is highlighted in gray.

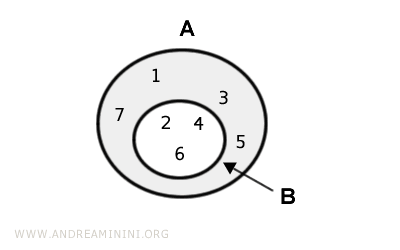
Properties of the Difference

Some properties of the difference between sets

• The difference between sets is not commutative $$ A-B \ne B-A $$

  Example. Let's consider two sets $$ A = \{ 0, 2, 4, 8, 10 \} $$ $$ B = \{ 2, 4, 6, 12 \} $$ The difference A-B is $$ A-B = \{ 0, 8, 10 \} $$ while the difference B-A is $$ B-A = \{ 6, 12 \} $$

• If the sets are disjoint sets, the difference A-B is equal to the first set A $$ A \cap B = Ø \Longleftrightarrow A-B= A $$

  Example. Let's consider two sets $$ A = \{ 2, 4, 6, 8 \} $$ $$ B = \{ 1, 3, 5, 7, 9 \} $$ The difference A-B is the set A $$ A-B = A = \{ 2, 4, 6, 8 \} $$ Here's the graphical representation
  
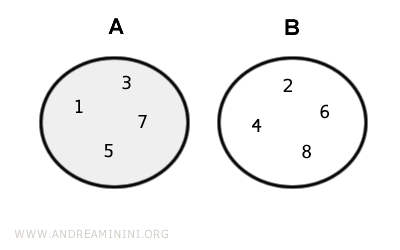
  Similarly, the difference B-A is equal to set B $$ B-A = B = \{ 1, 3, 5, 7,9 \} $$

• If the sets are equal sets, the difference A-B is the empty set $$ A = B \Longleftrightarrow A-B= Ø $$

And so on.