Set Cardinality

The cardinality of a set $ X $ indicates how many elements the set contains, denoted by $ |X| $.

The application of this concept goes beyond simple counting, particularly for infinite sets.

Cardinality of Finite Sets
The cardinality of a finite set is simply the count of its elements.
For example, consider a library housing a collection of books. If there are five books, the cardinality of this set of books is five, represented as $ |A| = 5 $, where $ A $ stands for the set of books.
Cardinality of Infinite Sets
With infinite sets, the concept of size becomes more nuanced.
Take, for instance, the set of natural numbers $ \mathbb{N} = \{ 0,1,2,3,... \} $ and the set of integers $ \mathbb{Z} = \{ ... -2, -1, 0, 1, 2, 3, ... \} $. Both sets are infinite with "countable" cardinality, meaning their elements can be arranged into an infinite sequence. Nonetheless, the natural numbers are a subset of the integers $ \mathbb{N} \subset \mathbb{Z} $. Another notable example is the set of real numbers $ \mathbb{R} $, encompassing all points on a continuous line, which exhibits "uncountable" cardinality because infinite points exist between any two distinct points. Thus, the integers are also a subset of the real numbers $ \mathbb{Z} \subset \mathbb{R} $, indicating an infinitely larger magnitude compared to $ \mathbb{N} $ or $ \mathbb{Z} $.

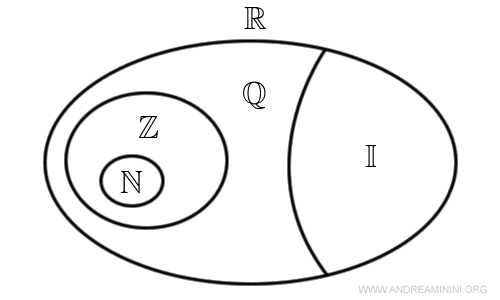
In essence, cardinality is not just a numerical measure of sets; it highlights the existence of different orders of infinity, unveiling a complexity that may not be initially apparent.

Observations

Additional insights and notes

Cardinality of Finite Sets
If A and B are finite sets, and A is a subset of B, then the number of elements (cardinality) of A will not exceed that of B, expressed as $ |A| \le |B| $. This reflects the principle that if set A is contained within set B, then A cannot have more elements than B. $$ A \subseteq B \Leftrightarrow |A| \le |B| $$
Example: Consider two sets $$ A = \{ 1, 2, 3 \} $$ $$ B = \{ 1, 2, 3, 4 \} $$ Clearly, A is a subset of B as all its elements are also in B $$ A \subseteq B $$ Set A has three elements, giving it a cardinality of |A|=3. Set B, containing four elements, has a cardinality of |B|=4. Hence, the cardinality of subset A is less than or equal to that of set B $$ |A| \le |B| $$
Cardinality of Equal Sets
If sets A and B are equal set ($ A=B $), they must contain an equal number of elements, thus sharing the same cardinality $ |A|=|B| $. This equality highlights that if two sets are exactly the same, their cardinalities will naturally match. $$ A = B \Rightarrow |A| = |B| $$
Example: Consider two finite sets A and B $$ A = \{1, 2, 3\} $$ $$ B = \{3, 1, 2\} $$ Both sets contain the same elements, albeit in a different order, making them identical and verifiable by $ A = B $. The cardinality of $ A $ is 3, since it includes three unique elements (1, 2, 3). Similarly, $ B $ also has a cardinality of 3 for the same reason. Therefore, sets A and B share the same cardinality. $$ |A| = |B| = 3 $$

And so forth.