Union of Sets

The union of two sets A and B is a set composed of elements that belong to set A, set B, or both.

The symbol for union is ∪.

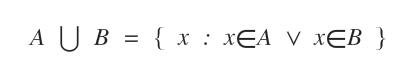
This is read as union of A and B or A union B.

If there are elements that belong to both sets, they are counted only once in the union set.

Union of Multiple Sets. The union operation can also be performed among multiple sets. To denote the union of a family of sets, write $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{for some}\:\: i \in I \} $$

A Practical Example

Consider two sets A and B.

Set A consists of the elements { 2, 5, 6, 7, 8 } while set B consists of the elements { 1, 3, 4, 6, 7, 9 }.

The union of the two sets AUB is the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

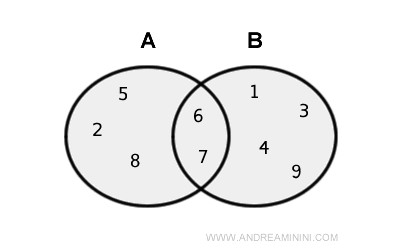
Note. Elements belonging to both sets {6, 7} are found in both set A and set B. Hence, there are two 6s and two 7s. However, in the union set A∪B, the elements 6 and 7 are considered only once because a set cannot have repeated elements.

Example 2

Consider two sets A and B.

$$ A = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

In this case, set B is a proper subset of A.

The union of the two sets is identical to set A.

$$ A U B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Common elements are included only once in the set A union B.

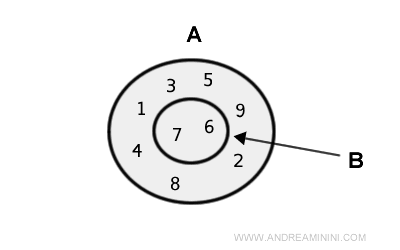
Example 2

Consider two sets A and B.

$$ A = \{ 1 , 3, 5, 7, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

In this case, the two sets are disjoint because they have no elements in common.

The union of the two sets includes all elements, both from set A and set B.

$$ A U B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Here is the representation of the sets using Euler-Venn diagrams.

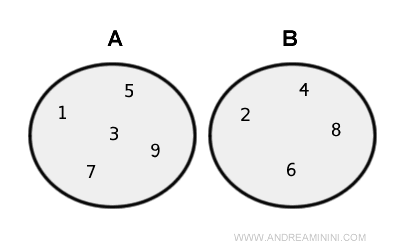
Note. Often, the union is likened to the OR conjunction (or) that is, to the logical disjunction. However, there are two types of logical disjunctions: inclusive or exclusive. The union can only be compared to the inclusive disjunction (inclusive OR) because it "includes" both alternatives. For example, if an element belongs to both A and B , it is included in the union set A∪B.

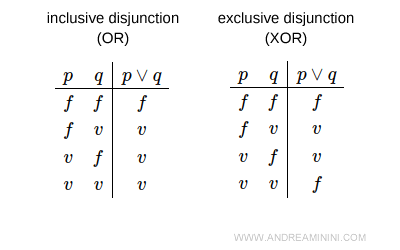
The union is different from the exclusive disjunction (exclusive OR or XOR), which excludes one of the two alternatives. In the exclusive disjunction, common elements of A and B would be excluded from the union set. Therefore, when comparing the union to the logical disjunction, it is necessary to specify inclusive disjunction.

Properties of Union

The operation of union between sets adheres to properties similar to those of addition and multiplication of numbers.

• Commutative Property
  Swapping the order of the sets does not change the union $$ A \cup B = B \cup A $$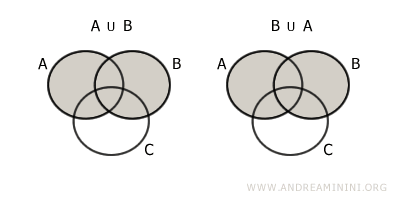

  

• Associative Property
  The union of A∪B with set C is the same as the union of set A with B∪C. $$ (A \cup B) \cup C = A \cup (B \cup C) $$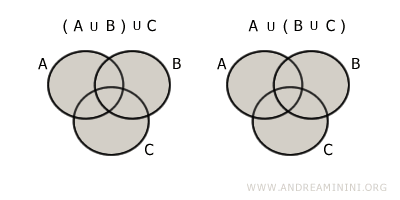

  

• Distributive Property of Union over Intersection
  The union of A with the intersection B⋂C is equal to the intersection of the unions A∪B and A∪C

  $$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$
  

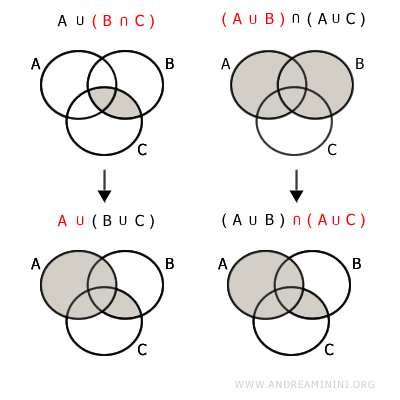
Cardinality of the Union Set

The cardinality of the union changes depending on whether the sets are disjoint or not.

• Disjoint Sets
  Disjoint sets have no elements in common. In this case, the cardinality of the union set is equal to the sum of the cardinalities of the sets $$ |A∪B|=|A| + |B| $$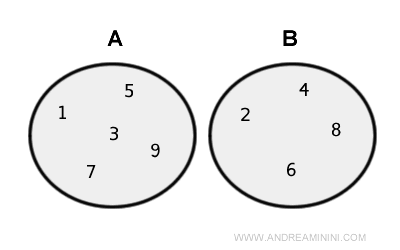

  

• Non-Disjoint Sets
  Non-disjoint sets have elements in common. In this case, the cardinality of the union is obtained from the sum of the two sets minus the cardinality of the intersection set. $$ |A∪B|=|A| + |B| - |A⋂B| $$
  

  

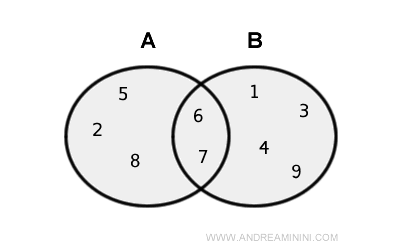
  Explanation. The sum of the elements of the sets counts the elements present in both sets, that is, the elements of the intersection A⋂B, twice. It is therefore necessary to subtract the elements of the intersection set A⋂B once to have the cardinality of the union set A∪B.

  

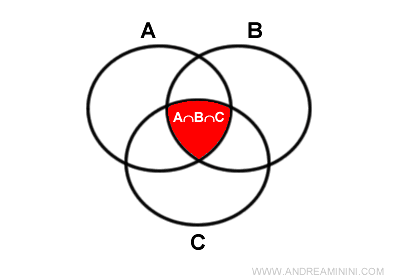
  If the non-disjoint sets are three, according to the principle of inclusion-exclusion, the cardinality of the union is $$ |A∪B∪C|=|A| + |B| + |C| - |A⋂B| - |A⋂C| - |B⋂C| + |A⋂B⋂C|$$

  Explanation. The sum |A|+|B|+ |C| counts the elements of the intersections |A⋂B|, |A⋂C|, |B⋂C| twice and the elements of the intersection |A⋂B⋂C| three times. Thus, I subtract them once from the count. However, this last exclusion removes the elements of the intersection |A⋂B⋂C| three times. For this reason, I must include them again.
  

And so on.