Difference Between Open and Closed Sets

The concepts of open and closed sets are crucial for understanding the structure of topological spaces. Generally, the difference lies in whether or not the set's boundaries are included within the set itself.

A closed set includes its boundaries, whereas an open set does not.

In other words, the boundaries of a closed set are elements of the set itself, while those of an open set are not.

Here's a general explanation of both concepts:

• Open Set

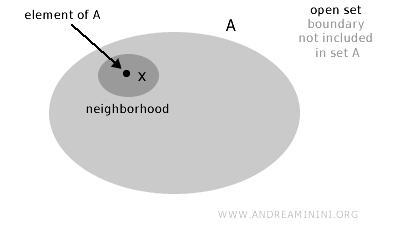
  An open set is one that does not include its "edges" or "boundaries".

  More formally, a set \(A\) in a topological space \(X\) is considered open if, for every point \(x\) in \(A\), there exists a neighborhood of \(x\) entirely contained in \(A\). This means that around every point of the set, one can find a "region" fully enclosed within the set, without having to "brush" against the outer boundary of the set.
  

  Example. A simple way to explain an open set is to imagine a set of real numbers between two extremes, such as 3 and 10. The open interval (3,10) consists of infinite real numbers 3<x<10 but does not include its endpoints 3 and 10 within. These endpoints are not part of the interval. It's a straightforward example of an open set seen in one dimension.
  

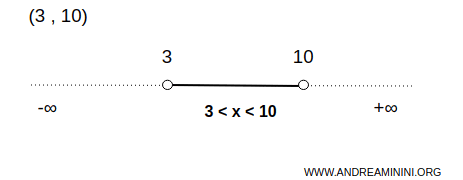
• Closed Set

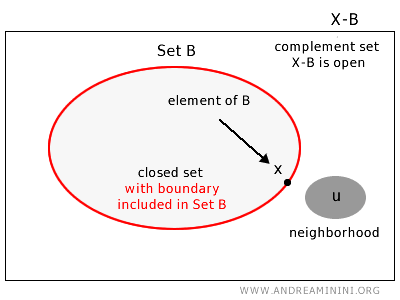
  A closed set is one that includes all its boundary points.

  Formally, a set \(B\) in a topological space \(X\) is said to be closed if, intuitively, its complement in \(X\), that is, the set of all points \(u \in X\) not belonging to \(B\), is an open set. Another significant characteristic of closed sets is that they contain all their accumulation points.
  

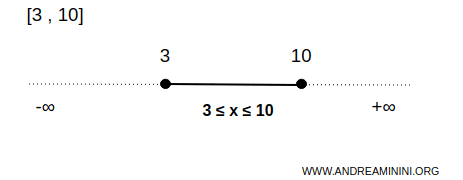
  Example. Taking the previous example of the set of real numbers between 3 and 10. Considering the closed interval [3,10], it includes infinite real numbers 3≤x≤10 but, unlike the open interval, it also includes its endpoints 3 and 10. In this case, 3 and 10 (the "boundaries") are elements of the set. Thus, there is no neighborhood of 3 and of 10 within set B. For instance, the neighborhood 3±0.01 is not part of set B because 3-0.01 equals 2.99 and is not part of B. It's a simple one-dimensional example of a closed set.
  

Why Distinguish Between Open and Closed Sets?

The notion of open and closed sets is central to many areas of mathematics, such as functional analysis, differential geometry, and the theory of topological groups, because it helps define and understand the internal structure of the spaces we work with.

Observations

Some side notes

• Clopen Sets and Sets that are Neither Open nor Closed
  It's important to note that in certain topological spaces, a set can be both open and closed, commonly known as a "clopen set." Additionally, there are sets that are neither open nor closed.

  For instance, in any topological space, the entire space itself and the empty set are always both open and closed. These two sets are the simplest examples of clopen sets.

And so on.