Clopen Sets

A set is called "clopen" if it is both open and closed within a given topology.

Essentially, a "clopen" set fulfills the criteria of being open and closed at the same time in the specified topology.

The term "clopen" combines "closed" and "open."

These sets exhibit characteristics of both open sets and closed sets.

This occurs when both a set and its complement are open in a particular topology.

Note: Clopen sets are quite uncommon in the real numbers but can exist in other topological spaces. They are fascinating because they offer unique properties and play a crucial role in understanding the topological structure of a space.

A Practical Example

Consider the set X={a,b,c,d} in topology T.

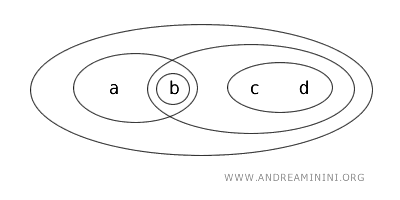
Under topology T, the following are considered "open sets": {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.

Therefore, the subset {a,b} qualifies as an "open set" under the same topology T.

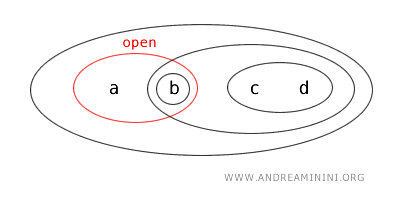
Interestingly, the set {a,b} is also the complement of the open set {c,d}

$$ X - \{ c,d \} = \{a , b \} $$

Since the complement of an open set is always a closed set:

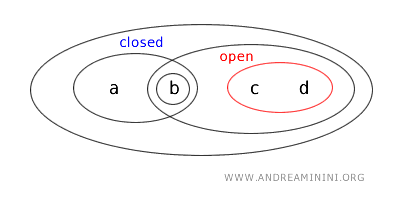
Hence, the set {a,b} is also a "closed set".

In conclusion, within topology T, the set {a,b} is both open and closed, making it a "clopen" set.

The Empty Set and the Entire Set are Clopen

In any topology on the set X, both the entire set (X) and the empty set (∅) are always considered clopen, meaning they are simultaneously open and closed.

For clarity, a set is deemed "clopen" if it qualifies as both open and closed within the considered topology.

Let's revisit the definitions of open and closed sets to better understand this concept.

According to the topological definition of an open set, both the empty set (∅) and the entire set (X) are invariably regarded as "open" sets.

Furthermore, as per the definition of a closed set, a set is considered "closed" if its complement is open.

Integrating these ideas, we can deduce that:

• Empty set (∅)
  By the fundamental principles of topology, the empty set is open. Concurrently, it is closed because its complement, X $ \setminus ∅=X $ (the entire set), is an open set. Therefore, it is both open and closed, or clopen.
• Entire set (X)
  The entire set is naturally open according to basic topological definitions. It is also closed because its complement, $ X \setminus X=∅ $ (the empty set), is an open set. Thus, it is both open and closed, or clopen.

Consequently, in every topology, both the entire set X and the empty set ∅ consistently qualify as clopen sets.

And so forth.