Discrete Topology

The discrete topology T is the largest possible topology on a set X, as it includes every possible subset of X.

In discrete topology, the collection of open sets T encompasses all possible subsets of X. Therefore, every subset of X is considered an open set.

This means that each individual element of X is deemed "open," thereby rendering every point "isolated" from the others.

In other words, there are no constraints on how close elements can be to one another; any configuration is allowed.

The discrete topology is termed "discrete" because it treats the elements of X as separate and distinct, without any "gradation" of closeness or continuity among them.

It is the largest topology that can be defined on a set, in the sense that there is no topology that contains more opens than the discrete one, since it already includes all possible subsets of X.

Note. These criteria establish a framework for open sets that allows us to discuss how elements of a space are "close" or can be connected without interruptions, i.e., continuity.

An essential feature of this topology is that:

In discrete topology, every subset of a topological space is both open and closed.

This unique property arises because the discrete topology considers all possible subsets of a space to be "open".

Consequently, the complement of any subset within the topological space is also an open subset.

In topology, a set is deemed closed if its complement is open.

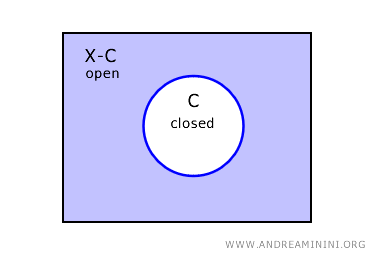
Thus, if the complement of every subset is open, then every subset is also closed.

This distinctive aspect of the discrete topology ensures that every subset is "clopen", meaning it is simultaneously closed and open, without exception.

Note. In discrete topology, this property holds for every subset, not merely for individual points. This occurs because each single point is considered an open set, as is any combination of points. Given that the complement of any possible subset is also a subset of the space and therefore open, every subset is invariably closed.

A Practical Example

Let's consider a simple example of discrete topology using a finite set X consisting of three elements.

$$ X = \{a, b, c\} $$

The power set of X, which is the set of all possible subsets of X, comprises the following subsets:

• The empty set: \(\emptyset\)
• Subsets with individual elements: \(\{a\}\), \(\{b\}\), \(\{c\}\)
• Subsets with two elements: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
• The entire set: \(\{a, b, c\}\)

In the discrete topology on X, every possible subset of X is considered an open set.

Therefore, the discrete topology \(T\) on \(X\) is given by:

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$

In this topology, every subset of \(X\) is open by definition.

Note. This is a topology because it includes the set X and the empty set. Moreover, any intersection and union of the open subsets remains part of the collection T. Since in a topology all subsets are open, it follows that there is no restriction on the proximity and continuity among the elements of the set X.

Take the subset $ \{ a \} $. By the definition of discrete topology, it is an open set.

Simultaneously, this subset $ \{ a \} $ is closed because its complement, $ X/ \{a\} = \{b,c\} $, is an open set. Remember, a closed set is simply the complement of an open set.

So, in discrete topology, the subset $ \{ a \} $ is both open and closed.

The same applies to every other subset in the topology.

And so on.