Open Sets
A set A is an open set if, for every element x within the set (x∈A), there exists a neighborhood that still belongs to the set.
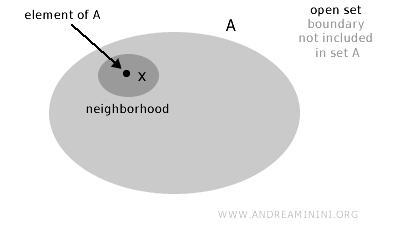
In other words, a set is considered open if, intuitively, its "boundaries" do not belong to the set itself.
More formally, a set A in a topological space X is open if, for every point x in A, there exists a neighborhood of x that is entirely contained within A.
Note. This means that around every point in the set, you can find a "region" that is fully enclosed within the set, without "touching" the outer boundary of the set.
A Practical Example
A simple example of an open set on a line is an open interval.
What is an open interval? An open interval on R is defined as the set of all points x such that a
This interval is denoted as (a,b), where the round brackets indicate that the endpoints a and b are not included in the set.
For instance, the open interval (3,10) is an open set on the real line.
In this case, set A consists of infinite numbers between 3 and 10, excluded.
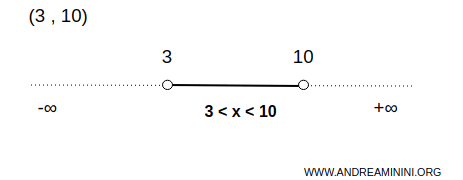
This means that for every point x within this interval, there is always a small open interval around x that is completely contained within (3,10).
For example, for the point x=3.1, I can take the open interval (3.09,3.11) which is entirely contained in (3,10).
The same applies to any other element within the interval (3,10), because between any two real numbers, there exist infinitely many real numbers.
Note. Even if I consider a very small real number within the interval (3,10), for example 3.001, I can still construct a neighborhood 3.001±0.00000001 that includes infinitely many real numbers within the open interval (3,10).
It's a simple one-dimensional example of an open set.
Other Examples
The same concept can be extended to two-dimensional space, such as the plane.
For example, the set of points of a circle with radius r=1 and center at the origin (0;0).
$$ x^2+y^2<1 $$
This inequality describes the set of all points whose distance from the center (0,0) is less than 1, hence NOT including the points on the circumference but only those inside the circle.
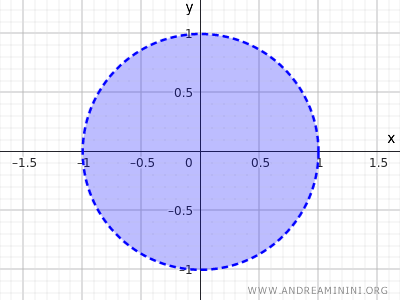
It's another example of an open set.
When is a set closed?
To have a closed set, simply include the points on the circumference in the set.
$$ x^2+y^2 \le 1 $$
In this case, the condition where every element of the set has a neighborhood contained within the set no longer applies.
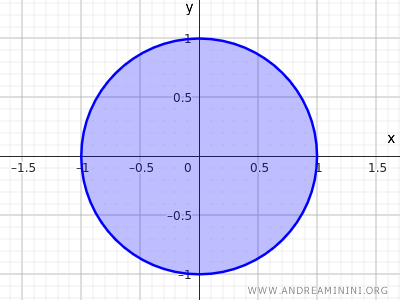
In the case of a closed set, the points on the circumference do not have a neighborhood entirely contained within the set.
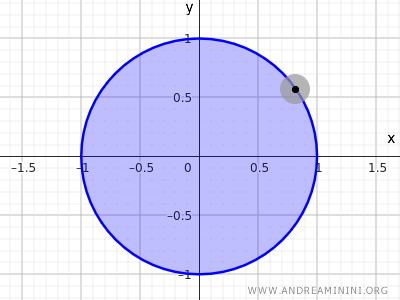
Note. In topology, the equation defining a circle $ x^2 +y^2=1 $ is neither an open nor a closed set in the Euclidean space R2 because it only considers the points on the circumference, without the points inside. Conversely, the set of points defined by the inequality $ x^2+y^2<1 $, which includes the internal points but not those of the circumference, is an example of an open set. Including also the points of the circumference $ x^2+y^2\le 1 $ would result in a closed set.
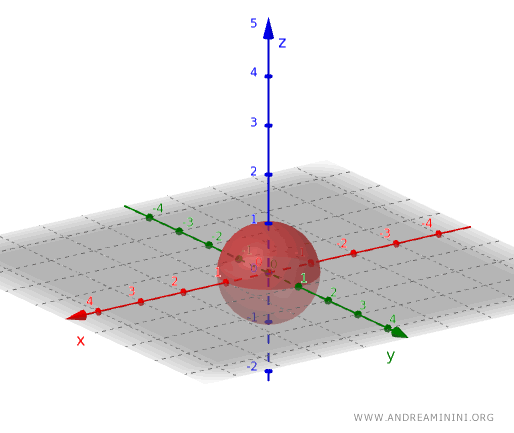
Applying the same principle, an open set in three-dimensional space can be created by considering, for example, the set of points located inside a sphere, excluding however those lying on its surface.
Choosing a Topology
Open intervals are very useful because they are intuitive and immediately give an idea of what an open set is.
However, the concept of an open set is much more abstract and should not be limited to just open intervals.
Therefore, once the concept is understood, it's appropriate to delve deeper into it.
The concept of an "open" set depends on the topology chosen to apply to a space.
The key idea to grasp is that the definition of open sets can drastically vary depending on the topology applied to a space.
In some spaces, a set that seems "closed" in a standard topology can be considered "open" in another topology.
In other words, any set can be considered open depending on the topology defined for a space.
What is a topology? A topology on a space is essentially a collection of sets considered "open" according to certain rules that these sets must satisfy, such as the arbitrary union of open sets being still an open set and the intersection of a finite number of open sets still being an open set.
For this reason, it is advisable not to limit thinking to the most common and intuitive examples of open sets, such as open intervals or open disks.
In topology, the definition of "open set" is much broader and can include sets that, at first glance, might not seem to be.
A Practical Example
Consider the space \( \{a, b\} \) containing only two elements.
In this space, at least two different topologies can be defined: the trivial topology and the discrete topology.
- Trivial Topology
In the trivial topology on \( \{a, b\} \), the only open sets are the empty set \( \emptyset \) and the space itself \( \{a, b\} \). This is the simplest possible topology, with practically no "open structure" beyond the total space and the empty set. - Discrete Topology
In the discrete topology, every possible subset of \( \{a, b\} \) is considered open. This means that \( \{a\} \), \( \{b\} \), \( \{a, b\} \), and \( \emptyset \) are all open. The discrete topology is the most "rich" in terms of open sets, as every combination of points forms an open set.
Now considering the set \( \{a\} \) in both topologies:
- In the trivial topology, the set {a} is not open
The only open set containing elements is \( \{a, b\} \), besides the empty set. - In the discrete topology, the set {a} is open
In this topology, every subset of \( \{a, b\} \), including \( \{a\} \) and \( \{b\} \), are open sets by definition.
Therefore, the set \( \{a\} \) is an open set under the discrete topology, but not under the trivial one.
This simple example highlights how the definition of an open set is closely tied to the chosen topology.
Open Set Theorem
Theorem 1
Given an open set X and a topology T that together form a topological space (X,T), a subset S⊂X is an open set in the topological space (X,T) if every element (or point) s∈S has a neighborhood U that is entirely contained within the subset S, meaning U⊂S.
By definition, S is an open set because it is part of the topological space (X,T).
Therefore, the subset S can be seen as the neighborhood of each of its elements (points) s∈S.
From this, I infer that the neighborhood Us of every element s∈S is, in turn, an open set contained within S.
$$ x \in U_s ⊂ S ⊂ X $$
An open set can be viewed as the union of open neighborhoods of its points.
Thus, if I observe that every element (point) s∈S of a subset S has a neighborhood Us⊂S contained within S, I can conclude that the set S is an open set because it is the union of open sets.
In other words, a set is open if and only if, for every point inside the set, there exists a neighborhood of that point which is completely contained within the set.
Example. Imagine a table scattered with glass marbles. Each marble represents a point within a certain set. Saying this set is "open" is akin to saying that there is enough space around each marble to move freely without crossing the table's edge. If for every marble on this table, I can draw a circle around it, entirely contained on the table (without touching the edges), then the set of marbles on the table represents an "open set". Essentially, the openness of the set means that no matter which marble I pick, there's always some "free" space around it that still belongs to the set of marbles on the table.

Theorem 2
Take a set \( X \) and a basis \( B \) for a topology on \( X \). A subset \( A \subset X \) qualifies as an open set in the topology generated by \( B \) if and only if, for every element \( x \) in \( A \), there's a basis element \( B_x \in B \) such that \( x \) is within \( B_x \) and \( B_x \) is completely contained in \( A \), meaning \( B_x \subseteq A \).
This theorem highlights a key characteristic of topologies formed by a basis.
Put simply, every point in an open set \( A \) must have a "neighborhood" around it, \( B_x \), that belongs to the basis sets and is fully enclosed by \( A \).
This confirms that the set \( A \) is indeed open in the topology created by \( B \).
Proof. If A is an open set in the topology generated by the base B on the set X, where A is a subset of X, then by definition, A is the union of the base elements. Consequently, every element x in A belongs to at least one base element Bx, and this Bx is entirely contained within set A, meaning Bx is a subset of A, since A is the union of the base elements. This reasoning can be reversed. If every element x in A is contained within at least one base element Bx that is entirely contained within A, or in other words, Bx is a subset of A, then the set A is open in the topology generated by B.
Example
Considering the set \( X = \{1, 2, 3, 4, 5\} \) and a basis for a topology on \( X \) as \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \), let's determine if the set \( A = \{1, 2, 3\} \) is open.
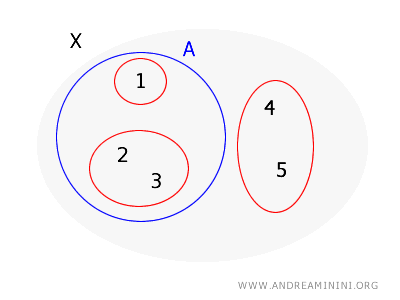
For every point in \( A \), I need to find a basis set that contains it and is entirely within \( A \):
- For point \( 1 \) in \( A \), there's the basis set \( \{1\} \) that contains \( 1 \) and is fully contained in \( A \).
- For point \( 2 \) in \( A \), the basis set \( \{2, 3\} \) contains \( 2 \) and is fully contained in \( A \).
- For point \( 3 \) in \( A \), the same basis set \( \{2, 3\} \) contains \( 3 \) and is entirely within \( A \).
Every point in \( A \) is included in a basis set that is, in turn, contained in \( A \), fulfilling the theorem's condition.
Thus, I can conclude that \( A \) is an open set in the topology generated by the basis \( B \).
Example 2
Considering the same set \( X = \{1, 2, 3, 4, 5\} \) and basis for a topology on \( X \) defined as \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) from the previous example.
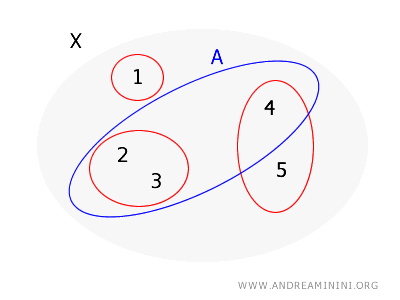
This time, however, I want to check if the set \( A = \{2, 3, 4\} \) is open.
- For point \( 2 \), I can use the basis set \( \{2, 3\} \), which is entirely within \( A \).
- For point \( 3 \), there's the same basis set \( \{2, 3\} \) covering it and fully within \( A \).
- For point \( 4 \), there's no basis set that contains it and is also completely inside \( A \) because the only basis set that includes 4 is \( \{4, 5\} \), which isn't fully inside \( A \) (since it includes 5, which isn't in \( A \)).
Therefore, according to the theorem, the set \( A \) is not an open set in the topology generated by the basis \( B \), because not every point in \( A \) has a basis set that is completely contained within \( A \).
Side Notes
Some remarks and side notes on open sets
- A set A is open if and only if A = Int(A)
A set \( A \) in a topological space \( X \) is open if it is equal to its interior. The interior of a set, denoted by Int(A), is the union of all open sets contained within \( A \). $$ A = \text{Int}(A) $$
And so forth.
