Path-Connected Spaces

A topological space S is path-connected if there is a continuous path linking any two points A and B within the space, without leaving the space.

Imagine a sheet of paper, disregarding the edges.

It represents a single continuous area and is considered open since it excludes the boundaries.

For any two points A and B on the paper, you can draw a line with a pen without lifting the pen from the surface.

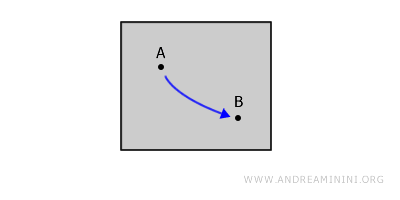
Put simply, the path does not exit the space containing the points A and B.

A path-connected space is inherently a connected space.

This might seem self-evident; if a space were disconnected, it would be split into separate parts, preventing any two points from being linked by a continuous path without exiting the space.

However, the reverse isn’t necessarily true. Not all connected spaces are path-connected.

Consider this scenario, which might seem counterintuitive but is entirely possible.

Take, for example, two sets, Q and T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

The first set, Q, consists of all the points along a sine wave defined for all real numbers R except zero, where it is undefined due to a division by zero—an undefined operation.

The second set, T, contains only the point zero.

The two sets Q and T are infinitely close to each other, as illustrated by the graph of the continuous function sin(1/x).

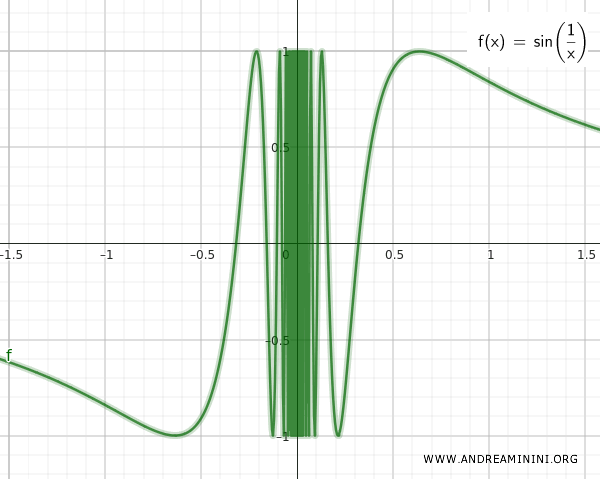
The set S is the union of sets Q and T.

$$ S = Q \cup T $$

Set S is connected because, for any ε>0, there is a neighborhood around zero (0-ε, 0+ε) that includes points from set Q.

This occurs because zero is a point of accumulation for the function sin(1/x).

Nevertheless, S is not path-connected because no arc exists that can connect any point from Q to zero (set T).

Note: The situation differs if the function were f(x)=1/x, because in this case, it is clear that the sets Q and T are disjoint, not infinitely close.

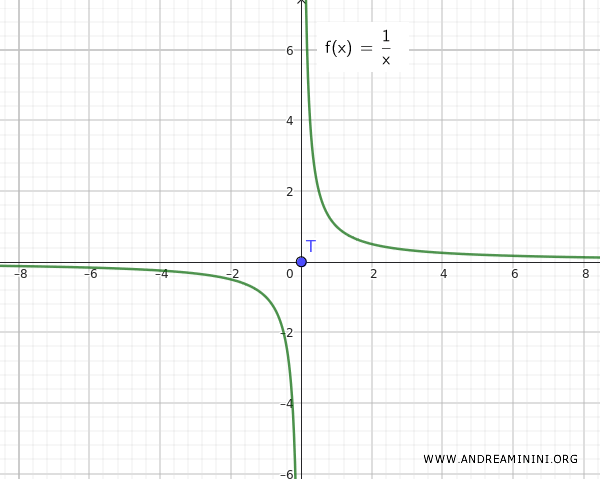
This example demonstrates that the union of a connected set Q={∀ x ∈ R-{0}, 1/x} and an isolated point T={0} does not necessarily create a connected set, unless the isolated point (e.g., zero) also serves as a point of accumulation.

 And so forth.