Interior of a Set

In a topological space $ X $, the interior of a set $ A $ is the union of all open subsets within $ A $. This is typically denoted by $ \text{Int}(A) $ or $ A^\circ $.

The interior of a set represents the largest open subset fully contained within $ A $.

No open subset within $ A $ is larger than the interior of $ A $.

Note: The nature of the interior stems directly from its definition as a union of open subsets, making it an open set itself.

Formally, the interior of the set $ A $ can be defined as the collection of all points in $ A $ around which there exists a completely enclosed open neighborhood within $ A $.

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ is open in } X \} $$

Essentially, for any point $ x $ within the interior of $ A $, there exists at least one open set $ U $ such that $ x $ is an element of $ U $, and $ U $ is contained within $ A $.

It's essential to remember that the interior of a set $A$ depends on the topological structure $X$ that contains set A, not on the properties of set A itself. Therefore, the interior of $A$ can vary depending on the topological structure $X$.

A Practical Example
The Interior Theorem of a Set
Interior Properties
Notes

A Practical Example

Consider the set $ A = [0, 1] $ within $ \mathbb{R} $ under standard topology.

This interval includes all real numbers from 0 to 1.

In this case, the interior of $ A $ is $ (0, 1) $.

$$ \text{Int}(A) = (0,1) $$

This is the largest open interval of points between 0 and 1, excluding the boundary points 0 and 1, which are not included in any open interval entirely within $ A $.

Example 2

Next, consider the set $ A = [0, 1) $ in $ \mathbb{R} $, again under the standard topology.

This interval includes all real numbers starting at 0 (inclusive) up to, but not including, 1, forming an interval that is closed on the left and open on the right.

Interestingly, the interior of $ A $ is still the open set $ (0,1) $, similar to the previous example:

\[ \text{Int}(A) = (0,1) \]

This occurs because the definition of an interior in a topological space involves the union of all open subsets that are completely contained within the original set.

Note: In $ \mathbb{R} $ with the standard topology, open intervals are the fundamental type of open sets. Therefore, the only maximal open set within $ [0, 1) $ is $ (0,1) $. It excludes the closed endpoint at 0, which is not part of any fully contained open interval. As a result, $ (0,1) $ encapsulates all the points in $ A $ that can be enclosed by open intervals fully within $ A $, thus satisfying the definition of an interior.

Example 3

In this example, we consider the set $ A = [0,1) $ under a discrete topology on $ X $.

In a space with discrete topology, each subset of $ X $ is deemed an open set.

This means that every element of $ A $ can be enclosed in a neighborhood that is entirely within $ A $, consisting of any combination of elements from $ A $.

With discrete topology on $ \mathbb{R} $, each subset is considered open. This includes all open and closed intervals, as well as any random combination of points, regardless of their distribution. Thus, open intervals like $ (0,0.5) $, $ (0.25,0.75) $, and $ (0,1) $ and closed intervals such as $ [0,0.25] $ within $ A=[0,1) $, as well as the empty set and the entire interval $ [0,1) $ itself, are open sets.

Since each subset is open, $ A = [0,1) $ itself is an open set in this topology.

Consequently, the interior of $ A $ in this context is $ A $ itself, since every point in $ A $ is part of an open subset that includes the point and is fully contained within $ A $.

$$ \text{Int}(A) = A = [0,1) $$

In a discrete topology, the interior of any set always matches the set itself.

Note: This example underscores how the selection of topology can influence the characteristics of neighborhoods and set interiors. As emphasized earlier, the features of a neighborhood depend on the topological structure $ X $ in which the set $ A $ is defined.

Example 4

Consider a topological space $ X $ consisting of points $ \{a, b, c\} $, with a discrete topology applied to $ X $.

In this setting, every subset of $ X $ qualifies as open:

By definition, $ \emptyset $ and $ \{a, b, c\} $ are open in $ X $.
Individual points such as $ \{a\} $, $ \{b\} $ and $ \{c\} $ are open since each point is considered an open set in discrete topology.
Subsets composed of point pairs, like $ \{a, b\} $, $ \{a, c\} $, $ \{b, c\} $ are open as they are combinations of open sets.

Considering the set $ A = \{b, c\} $ within $ X $:

According to the definition of an interior, $ \text{Int}(A) $ is the union of all open subsets contained in $ A $.

The open subsets within $ A $ are $ \{b\} $, $ \{c\} $, and $ \{b, c\} $.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Hence, the union of these open subsets is $ \{b, c\} $, precisely matching $ A $.

In conclusion, $ \text{Int}(A) = A $ holds true.

Note: This result isn’t specific to $ A $; it applies universally to any subset $ S \subseteq X $ in a discrete topological space. In such a space, every subset is open, meaning the interior of any set $ S $ is $ S $ itself, i.e., $ \text{Int}(S) = S $.

The Interior Theorem of a Set

In a topological space $X$, for a subset $S$ and an element $y \in X$, the element $y$ belongs to the interior of $S$, denoted $\text{Int}(S)$, if and only if there exists an open set $U$ such that $y \in U \subseteq S$. Mathematically, $$ y \in \text{Int}(S) \iff \exists \ U \text{ open, with } y \in U \subseteq S $$

Put simply, an element $y \in X$ is considered to be within the neighborhood of the set $S$ if it also lies within an open set $U$ that is fully enclosed by $S$.

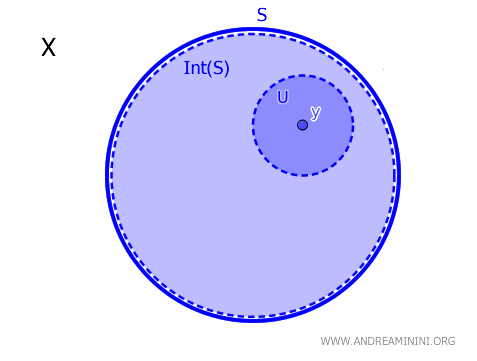
visual example

This theorem provides a necessary and sufficient condition for determining whether a point $y$ resides within a set $S$ in a topological space $X$.

Proof

Necessary condition: If $y$ is within the interior of $S$, by definition, there exists an open set $U$ in $X$ such that $y$ is included in $U$ and $U$ is entirely within $S$. This confirms that if $y \in \operatorname{Int}(A)$, such $U$ must exist, satisfying the "only if" condition of the theorem.
Sufficient condition: If an open set $U$ exists such that $y \in U \subseteq S$, then by the nature of open sets and the fact that $U$ lies within $S$, all points in $U$, including $y$, are by definition part of the interior of $S$, since the interior is defined as the union of all open sets contained within $S$. Hence, $y$ necessarily belongs to $\operatorname{Int}(S)$.

Note: This theorem is crucial as it directly relates the concept of an open set to being within a set, which is pivotal in exploring continuity and other topological characteristics of spaces.

Example

Consider the set $ A = [1, 3] $ of real numbers within the closed interval from 1 to 3 in the topological space $ \mathbb{R} $ under the standard topology.

$$ A = [1,3] $$

Effectively, this encompasses all points along the segment from 1 to 3.

I will determine the interior of $ A $ using the interior theorem of a set.

To ascertain the interior of $ A $, I must identify an open set $ U $ such that $ U \subseteq A $ and every point within $ U $ is also within $ \operatorname{Int}(A) $.

Selection of $ U $
I select $ U = (1, 3) $, the open interval from 1 to 3 excluding the endpoints. This set is open under the standard topology of $ \mathbb{R} $ because it is an open interval.
Verification that $ U \subseteq A $
I note that every point in $ U = (1, 3) $ also lies within $ A = [1, 3] $, with the exception of the endpoints $ 1 $ and $ 3 $ which are excluded because $ U $ is an open set and does not encompass its endpoints.

Thus, $ U $ is an open set fully contained within $ A $, meaning all points of $ U $ are internally part of $ A $. In this scenario, the interior of $ A $, $ \operatorname{Int}(A) $, is precisely $ (1, 3) $.

Note: This finding illustrates that the interior of $ A $ is the open interval $ (1, 3) $. Points at the boundaries $ 1 $ and $ 3 $ are not included in $ \operatorname{Int}(A) $ because no open interval that contains these points is fully enclosed within $ A $.

Interior Properties

This section delves into various properties associated with the interior of sets in a topological space. Each property uncovers a fascinating, and sometimes counterintuitive, relationship between fundamental topological operations such as interiors, closures, unions, and intersections.

Union of Interiors Property
The union of the interiors of two sets is always contained within the interior of their union. However, this containment does not necessarily mean the two are equal. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Intersection of Interiors Property
The intersection of the interiors of two sets is exactly the interior of their intersection. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
Interior of the Complement and Complement of the Closure
The interior of the complement of a set $A$ is identical to the complement of the closure of $A$. $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
Closure of the Complement and Complement of the Interior
The closure of the complement of a set $A$ is the same as the complement of the interior of $A$. $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Notes

Some margin annotations and additional notes

If U is an open set in X and U ⊆ A, then U ⊆ Int(A)
If $ U $ is an open set within a topological space $ X $ and is entirely contained within another set $ A $, then $ U $ is also included in the interior of $ A $. The interior of $ A $, denoted $ \text{Int}(A) $, is defined as the largest open set contained within $ A $. Therefore, any open set $ U $ that lies within $ A $ automatically becomes a part of the interior of $ A $.
If A ⊆ B, then Int(A) ⊆ Int(B)
If a set $ A $ is fully contained within another set $ B $, then the interior of $ A $ must also be contained within the interior of $ B $. This is because any open set within $ A $ will also be contained within $ B $. Thus, the operation of forming an interior preserves the inclusion relationship between sets.
A set A is open if and only if A = Int(A)
A set $ A $ in a topological space $ X $ is defined as open if it coincides with its interior. In other words, $ A $ is open if every point in $ A $ has an open neighborhood fully contained within $ A $. Therefore, $ A $ is open if and only if $ A = \text{Int}(A) $, meaning it encompasses all the open sets it can potentially contain within itself.
To find the interior of a set, I can create a script using the R programming language
R is particularly well-suited for mathematical and statistical computations, making it an ideal choice for this task. By leveraging R's powerful functions, I can efficiently compute and analyze the interiors of sets within a topological space.

And so forth.