Topology of Open Sets

In other words, the collection T must only include subsets of X considered "open" and is closed under the operations of union and intersection.

Where a collection of sets is a set whose elements are sets or subsets.

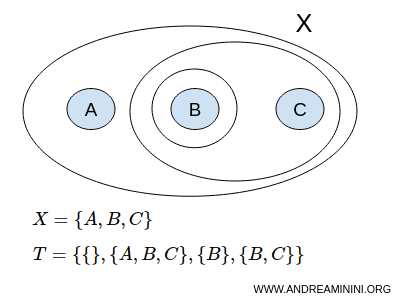
In these instances, the set X and the topology T constitute a topological space, often denoted as the pair (X,T).

Note. For simplicity, it's often said that X is a topological space. However, it's important to remember that a topological space consists of two elements: the topology T (collection of subsets) and the set X.

Why is the empty set always considered an open set?

The empty set is considered open by definition in every topological space.

This convention is a fundamental part of topology definitions and ensures the properties and axioms of topology are consistent and complete.

A Practical Example

Consider a set X with three elements A, B, C

$$ X = \{ A,B,C \} $$

A topology T could be the collection of subsets { }, {A,B,C}, {B}, {B,C}

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

Where { } represents the empty set Ø, and {A,B,C} is the set itself, or the improper subsets of set X.

By definition, the empty set and the complete set X are open sets.

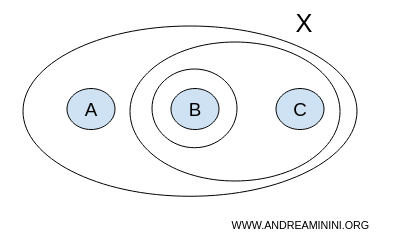
A topology must be composed of open sets and, by definition, the union and intersection of open sets yield another open set.

In this case, the union of subsets considered in T still belongs to the collection T.

Thus, the collection T is closed to union operations.

$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$

$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$

$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$

$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$

Furthermore, the intersection of subsets in T remains part of the collection T.

Therefore, the collection T is also closed to intersection operations.

$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$

$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$

$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$

$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$

Therefore, the collection T is a topology of set X because it meets all necessary conditions.

Example 2

Consider a slightly different collection from the previous example.

The set X remains the same.

$$ X = \{ A,B,C \} $$

In this case, however, the collection T also includes the subset {A} in addition to the subsets { }, {A,B,C}, {B}, {B,C}.

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

This new collection T of subsets is not a topology of set X because it does not satisfy all conditions.

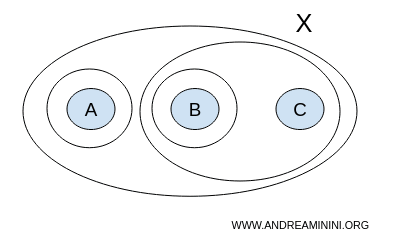
For example, the union of subsets {A} and {B} creates a set {A,B} that is not included in the collection T itself.

$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T  $$

In other words, the two sets {A} and {B} are considered "open" sets because they are found in the collection T.

However, their union does not create another open set {A,B} because the set {A,B} is not found in the collection.

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

This violates one of the necessary conditions for the topology of an open set.

Therefore, the collection T cannot be considered a topology of set X.

And so on