Sets Neither Open Nor Closed

In topology, a set that is neither open nor closed does not fulfill the requirements of either category.

This phenomenon can occur in a topology where the set is neither defined as an open set nor is it the complement of one.

Therefore, the set is also not a closed set.

Note: Such sets might be hard to visualize within the familiar topology of real numbers. However, they are completely feasible in more complex topological structures. A practical example would help clarify this concept.

    A Practical Example

    Consider the set X={a,b,c,d} and topology T, which defines the following open sets: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, and Ø.

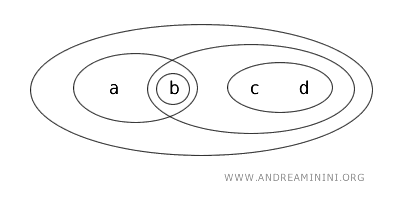
    a practical example

    Let’s examine the subset {b,c} of the set X.

    • The set {b,c} is not an "open set" because topology T does not explicitly define it as such.
    • Similarly, {b,c} is not the complement of any open set within topology T, and thus it is not a "closed set" either.

    In conclusion, according to topology T, the set {b,c} is neither open nor closed.

    And so forth.

     
     
    Please feel free to point out any errors or typos, or share suggestions to improve these notes. English isn't my first language, so if you notice any mistakes, let me know, and I'll be sure to fix them.

    Quick Answers

    • In the topology of real numbers, it seems quite common to encounter sets like [0, 1), which are neither open nor closed. Is that correct?
      The interval \([0, 1)\) in the topology of real numbers (with the standard topology) is:
      • Not Open: An interval is open if every point inside it has a neighborhood fully contained within the interval. In \([0, 1)\), the point \(0\) does not have such a neighborhood because every neighborhood of \(0\) includes points less than \(0\), which are not part of the interval.
      • Not Closed: An interval is closed if it contains all its limit points. The point \(1\) is a limit point of \([0, 1)\), but \(1\) is not included in the interval, so \([0, 1)\) is not closed.
      Therefore, you're correct that \([0, 1)\) is neither open nor closed in the standard topology on \(\mathbb{R}\). It is an example of a half-open or semi-open interval.

     

    FacebookTwitterLinkedinLinkedin
    knowledge base

    Topology

    Exercises