Open Rectangle Topology
Open rectangle topology forms a key topological framework within the R2 plane, where open sets are characterized as any union of open rectangles. Each rectangle is a product of two open intervals along the Cartesian axes, creating a structure that lays the foundation for understanding spatial relationships in two dimensions.
This topology is defined by a base consisting entirely of open rectangular neighborhoods, effectively using these shapes as the building blocks for more complex spatial constructs.
To put it another way, a set \( U \subseteq \mathbb{R}^2 \) qualifies as open if, for every point \( (x, y) \) it contains, you can find an open rectangle that not only encompasses \( (x, y) \) but also fits entirely within \( U \).
Open rectangles thus serve as the essential components for constructing the topology of the Euclidean plane.
$$ B= \{ (a, b) \times (c, d) | a<b, c<d \} $$
Where \( a, b, c, d \) represent real numbers, with \( a < b \) and \( c < d \), delineating the bounds of these rectangles.
This approach provides an alternate basis for the \( \mathbb{R}^2 \) plane, contrasting with the standard topology typically defined by circles.
Note: This highlights the versatility of topological foundations, demonstrating that various shapes, whether circles or rectangles, can serve as a basis without affecting the overarching definition of open sets. Regardless of the shape, the aggregation of these open sets forms a cohesive basis for the topology of \( \mathbb{R}^2 \).
An Open Rectangle Example
An open rectangle in the \( \mathbb{R}^2 \) plane is essentially a cartesian product of two open intervals, one along each axis.
Consider, for example, the open intervals \( (1, 3) \) along the \( x \)-axis and \( (2, 4) \) along the \( y \)-axis.
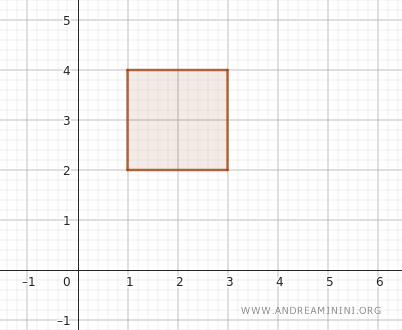
The open rectangle that emerges from these intervals consists of all points \( (x, y) \) where \( x \) lies between 1 and 3, and \( y \) is nestled between 2 and 4.
Formally, this rectangle is expressed as \( (1, 3) \times (2, 4) \).
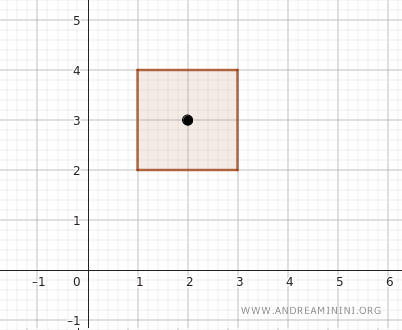
So, picking any point within this space, such as \( (2, 3) \), illustrates that the point’s \( x \)-coordinate is greater than 1 but less than 3, and its \( y \)-coordinate exceeds 2 but remains under 4.
Note: The periphery of the rectangle is excluded from the set, leaving points like \( (1, y) \), \( (3, y) \), \( (x, 2) \), and \( (x, 4) \) outside the bounds of the open rectangle.
