Product Topology of Topological Spaces

Given two topological spaces $X$ and $Y$, the product topology on $X \times Y$ is defined as the topology generated by the basis $B$, which consists of the Cartesian products of all open sets of the form $U \times V$, where $U$ is open in $X$ and $V$ is open in $Y$. $$ B = \{ U \times V \mid U \text{ is open in } X \text{ and } V \text{ is open in } Y \} $$

The initial idea for creating a topology on $X \times Y$ is to consider sets of the form $U \times V$, where $U$ is an open set in $X$ and $V$ is an open set in $Y$.

This collection of sets is denoted by $B$ and forms a basis for a topology.

A basis for a topology is a collection of open sets such that every other open set in the topological space $X \times Y$ can be written as a union of these basis sets.

In the product topology, the Cartesian product of open sets remains an open set.

Note: The open sets in the product topology are not limited to the Cartesian products $X \times Y$ of open sets from $X$ and $Y$; they also include all possible unions of these products. Because of this, the collection $B$ is not considered a complete topology, but rather a basis for the product topology. If $B$ were treated as a full topology, it would not encompass all open sets that can be formed by taking unions of Cartesian products.

The same principle holds true for closed sets.

In the product topology, the Cartesian product of closed sets remains a closed set.

Similarly, not all closed sets in the product topology can be expressed as the product of closed sets.

In other words, just as with open sets, there can be closed sets in the product topology that are not derived from the Cartesian product of closed sets.

A Practical Example
The Product of Multiple Topological Spaces
The Basis of Product Topology
Notes

A Practical Example

Let's go through a concrete example to clarify the concept of product topology.

Suppose we have two simple topological spaces:

$X$ is the real line $\mathbb{R}$ with the standard topology (open sets are open intervals $(a, b)$).
$Y$ is also the real line $\mathbb{R}$ with the same standard topology.

Now, consider the product $X \times Y$, which generates the Cartesian plane $\mathbb{R} \times \mathbb{R} = \mathbb{R}^2$.

To construct the basis $B$ of the product topology on $X \times Y$, we take all the products $U \times V$ where $U$ is an open set in $X$ and $V$ is an open set in $Y$.

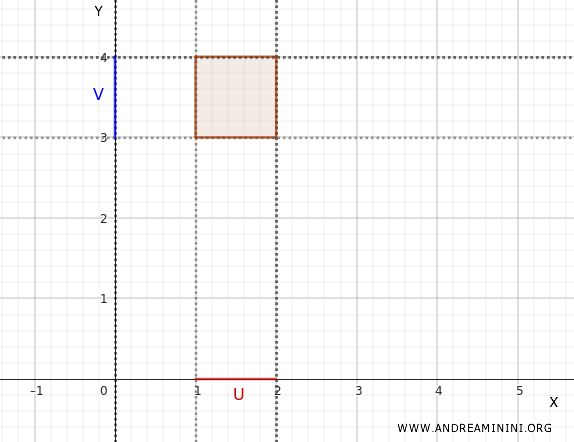
For example, let $U = (1, 2) \subset X$, an open interval in $X$.

Then, let $V = (3, 4) \subset Y$, an open interval in $Y$.

Thus, $U \times V = (1, 2) \times (3, 4)$ is an open set in $\mathbb{R}^2$. This set is an open rectangle in the Cartesian plane $\mathbb{R}^2$.

example

Let's examine what happens when we take the union of two basis sets.

Consider $U_1 \times V_1 = (1, 2) \times (3, 4)$.

Then consider $U_2 \times V_2 = (1.5, 2.5) \times (3.5, 4.5)$.

These sets represent two open rectangles in the plane.

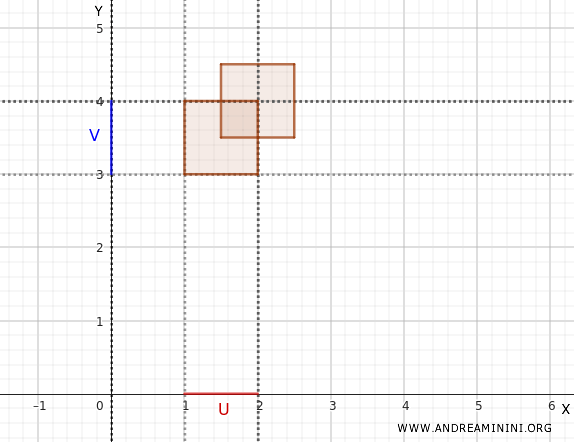
an example of the union of open sets

Their union does not take the typical form of the Cartesian product $U \times V$, but it is still a union of basis sets and therefore represents an open set in the product topology:

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

In this way, every point in the plane can be covered by a union of basis sets $U \times V$.

For example, let's check if the point $(1.8, 3.8)$ is covered by this basis.

The product $ (1, 2) \times (3, 4) $ contains the point $(1.8, 3.8)$. Therefore, $(1.8, 3.8)$ belongs to the union of the basis sets.

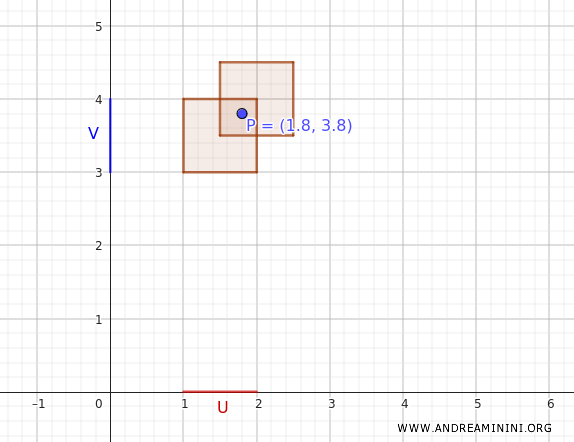
example

This example confirms that the basis $B$ generates a valid topology on the Cartesian product $X \times Y$ of topological spaces.

Note: This topology is called the "product topology" and is particularly useful because it preserves the open structure of the original spaces $X$ and $Y$ in the product $X \times Y$.

Example 2

Consider two topological spaces:

$X = \{a, b, c\}$ with the topology $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$ with the topology $\{\emptyset, \{1\}, Y\}$

To compute the product topology on $X \times Y$, we take all the Cartesian products of the open sets in the topologies of $X$ and $Y$ and then consider all possible unions of these products.

$$ B = \{ U \times V \mid U \text{ is open in } X \text{ and } V \text{ is open in } Y \} $$

The open sets of $X$ are:

$\emptyset$
$\{a\}$
$\{b, c\}$
$X = \{a, b, c\}$

The open sets of $Y$ are:

$\emptyset$
$\{1\}$
$Y = \{1, 2\}$

Now, we compute the Cartesian products of these sets:

$\emptyset \times \emptyset = \emptyset$
$\emptyset \times \{1\} = \emptyset$
$\emptyset \times Y = \emptyset$
$\{a\} \times \emptyset = \emptyset$
$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \emptyset = \emptyset$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times \emptyset = \emptyset$
$X \times \{1\} = \{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Note: The Cartesian product of sets is defined as the set of ordered pairs where the first elements belong to the first set and the second elements belong to the second set. Formally, the Cartesian product $A \times B$ is defined as: \[ A \times B = \{(a, b) \mid a \in A \text{ and } b \in B\} \] Now, if one of the sets is the empty set ($\emptyset$), there are no elements in this set to pair with elements from the other set. Consequently, there cannot be ordered pairs where at least one element comes from the empty set. Therefore, the Cartesian product of $\emptyset$ with any set $B$ is the empty set. \[ \emptyset \times B = \{(a, b) \mid a \in \emptyset \text{ and } b \in B\} = \emptyset \] In other words, since there are no elements $a \in \emptyset$, there can be no pairs $(a, b)$ with $b \in B$. For example, \[ \emptyset \times \{1\} = \emptyset \] This is why the Cartesian product of the empty set with any set is the empty set.

The product topology is the set of all possible unions of these Cartesian products. Therefore, the product topology on $X \times Y$ includes:

$\emptyset$
$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$
Any other union of these sets
For example, $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$, etc.

The product topology on $X \times Y$ thus consists of all these unions.

This confirms that in the product topology, open sets are not just the products of the open sets $X \times Y$; sets obtained by the union of Cartesian products are also open.

For example, this union of sets is an open set in the product topology: $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$. Therefore, it is incorrect to think that only the products $X \times Y$ are open sets in the product topology.

The basis $B$ of the topology $X \times Y$ consists only of non-empty Cartesian products.

$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

The Product of Multiple Topological Spaces

This concept can also be applied to the product of multiple topological spaces.

Given $ n $ topological spaces $ X_1 $, $ X_2 $, up to $ X_n $, if $ U_i $ is a collection of open sets in each space $ X_i $, then the collection of all possible products of these open sets $ U_1 \times U_2 \times \cdots \times U_n $ forms a basis for a new topology on the product space $ X_1 \times \cdots \times X_n $. $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ is open in } X_i \text{ for each } i \} $$

The Basis of Product Topology

In general, the Cartesian product of open sets from two topological spaces provides a valid basis for the product topology.

$$ B = \{ U \times V \mid U \text{ is open in } X \text{ and } V \text{ is open in } Y \} $$

However, this basis can become quite large in practice.

There is an alternative approach to creating a more compact and efficient basis for the product topology.

Given two topological spaces $ X $ and $ Y $ with bases $ B_X $ for the topology on $ X $ and $ B_Y $ for the topology on $ Y $, the basis for the product topology on $ X \times Y $ is constructed from the Cartesian product of these bases: $$ B = \{ U \times V \mid U \in B_X \text{ and } V \in B_Y \} $$

This set $ B $ forms a basis for the product topology on $ X \times Y $.

In other words, the elements of $ B $ are the basic open sets of the product topology, and any open set in this topology can be expressed as a union of these Cartesian products $ U \times V $.

Note. This concept can be extended to the product of any number of topological spaces. Given $ n $ topological spaces $ X_1 , X_2 , ... , X_n $, if $ B_i $ is a basis for each space $ X_i $, then the products of these bases form a basis for the product topology on $ X_1 \times X_2 \times \cdots \times X_n $. $$ B = \{ B_1 \times \cdots \times B_n \ \ \mid \ \ B_i \text{ is a basis for } X_i \text{ for } i = 1, \ldots, n \} $$

Example

Let's consider two topological spaces:

The topological space $ X = \{a, b\} $ with the topology $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $ has a minimal basis $ B_X = \{\{a\}, \{b\}\} $.
The topological space $ Y = \{1, 2\} $ with the topology $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $ has a minimal basis $ B_Y = \{\{1\}, \{2\}\} $.

We can construct a minimal basis for the product topology by considering only the Cartesian products of the elements in $ B_X $ and $ B_Y $, instead of all open sets in each topological space.

$$ B_X = \{\{a\}, \{b\}\} $$

$$ B_Y = \{\{1\}, \{2\}\} $$

The Cartesian products of these two bases are:

$$ \{a\} \times \{1\} = \{(a, 1)\} $$

$$ \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\} $$

$$ \{b\} \times \{2\} = \{(b, 2)\} $$

Therefore, the minimal basis for the product topology on $ X \times Y $ is:

$$ B_{\text{min}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

This minimal basis is sufficient to generate the entire product topology on $ X \times Y $.

Every open set in the product topology can be expressed as a union of these minimal basis sets.

In essence, by using only the Cartesian products of atomic sets (those that cannot be decomposed further), we obtain a smaller basis for the product topology that still fully describes the topology.

Proof

I aim to demonstrate that the set $ B $ serves as a basis for the product topology on $ X \times Y $.

$$ B = \{U \times V \mid U \in B_X \text{ and } V \in B_Y\} $$

Here, $ B_X $ is a basis for the topology on $ X $, and $ B_Y $ is a basis for the topology on $ Y $.

In the product topology, open sets are unions of sets of the form $ U \times V $, where $ U $ is open in $ X $ and $ V $ is open in $ Y $.

To prove that $ B $ is indeed a basis for this topology, we must show that every open set $ W $ in $ X \times Y $ can be expressed as a union of elements from $ B $.

Verification of the Basis Property

Suppose $ W $ is an open set in the product topology on $ X \times Y $, and $ (x, y) $ is a point in $ W $.

By definition of the product topology, there exist open sets $ U' \subseteq X $ and $ V' \subseteq Y $ such that:

$$ (x, y) \in U' \times V' \subseteq W $$

Since $ U' $ is open in $ X $ and $ B_X $ is a basis for the topology on $ X $, there exists an element $ U \in B_X $ such that:

$$ x \in U \subseteq U' $$

Likewise, since $ V' $ is open in $ Y $ and $ B_Y $ is a basis for the topology on $ Y $, there exists an element $ V \in B_Y $ such that:

$$ y \in V \subseteq V' $$

Therefore, we can conclude:

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

This shows that for every point $ (x, y) $ in $ W $, there is an element $ U \times V $ in $ B $ such that $ (x, y) $ belongs to $ U \times V $ and $ U \times V $ is contained within $ W $.

Conclusion

Since every point $ (x, y) $ in an open set $ W $ in the product topology lies within some element of the basis $ B $ that is also contained within $ W $, it follows that $ B $ covers all open sets in the product topology.

Hence, the set $ B = \{U \times V \mid U \in B_X \text{ and } V \in B_Y\} $ is indeed a basis for the product topology on $ X \times Y $.

This concludes the proof.

Notes

Some additional notes on product topology

Product Subspace Theorem
This theorem states that if you take two subspaces $A$ and $B$ of topological spaces $X$ and $Y$, the topology on their product $A \times B$, considered as a subspace of $X \times Y$, is identical to the product topology on $A \times B$ that is derived from the individual topologies on $A$ and $B$. In other words, regardless of how you construct the topology on $A \times B$, the resulting topological structure will be the same. $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Topological Equivalence of Product Space
Given three spaces $ X $, $ Y $, and $ Z $, the products $ (X \times Y) \times Z $, $ X \times (Y \times Z) $, and $ X \times Y \times Z $ are topologically equivalent. In other words, no matter how you group them, the resulting topological space remains the same. $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
The Interior Theorem for Cartesian Products
Given two sets $A$ and $B$ that belong to the topological spaces $X$ and $Y$ respectively, the interior of their Cartesian product $A \times B$ is equal to the product of the interiors of $A$ and $B$. $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

And so forth.