Theorem on the Interior of the Cartesian Product

Given two sets \(A\) and \(B\) within two topological spaces \(X\) and \(Y\) respectively, the interior of their Cartesian product \(A \times B\) is equal to the product of their interiors. In other words: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

This property specifically applies to open sets in the context of the product of two topological spaces.

In simpler terms, this theorem tells us that for sets \(A\) and \(B\) in topological spaces \(X\) and \(Y\), the interior of their Cartesian product can be determined by taking the product of the interiors of \(A\) and \(B\).

A Practical Example

Let's consider two topological spaces \(X = \mathbb{R}\) and \(Y = \mathbb{R}\), and two subsets \(A = (0, 2)\) and \(B = (1, 3)\).

Here, \(A\) and \(B\) are open intervals on the real line \(\mathbb{R}\).

First, let's find the interiors of these two sets.

The interior of \(A\) is simply (0,2), since \(A\) is already an open interval, meaning its interior is \(A\) itself.

$$ \text{Int}(A) = (0, 2) $$

Similarly, the interior of \(B\) is (1,3).

$$ \text{Int}(B) = (1, 3) $$

Now, let's calculate the Cartesian product of the interiors \(\text{Int}(A) \times \text{Int}(B)\):

$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$

This Cartesian product is the set of all pairs \((x, y)\) where \(x \in (0, 2)\) and \(y \in (1, 3)\).

$$ \text{Int}(A) \times \text{Int}(B) = \{(x, y) \mid x \in (0, 2) \text{ and } y \in (1, 3)\} $$

This set can also be visualized as an open rectangle in the plane \(\mathbb{R}^2\), defined by the corners \((0, 1)\), \((0, 3)\), \((2, 1)\), and \((2, 3)\).

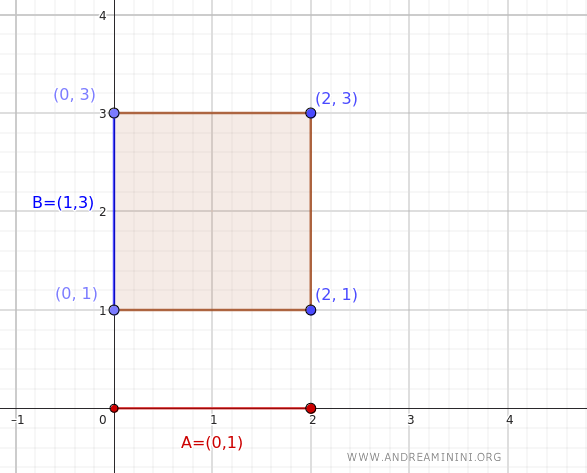
Now, let's calculate the interior of the Cartesian product \(A \times B = (0, 2) \times (1, 3)\):

We get the same set as before, the open rectangle in the plane \(\mathbb{R}^2\).

The interior of the Cartesian product \(\text{Int}(A \times B)\) is exactly equal to the product of the interiors \(\text{Int}(A) \times \text{Int}(B)\).

$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$

This example verifies the theorem.

Proof

The proof is divided into two parts. First, we'll show that the interior of the Cartesian product contains the product of the interiors, and then we'll demonstrate that it's contained within the product of the interiors, thereby proving their equality.

1] The Interior of the Cartesian Product Contains the Product of the Interiors

In this first part, we need to prove that

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

In other words, we need to show that every pair \((x, y)\) where \(x \in \text{Int}(A)\) and \(y \in \text{Int}(B)\) belongs to the interior of \(A \times B\).

Since \(x \in \text{Int}(A)\) is an element of the interior of \(A\), we know there exists an open set \(U\) contained within \(X\) such that \(x \in U \subseteq A\).

Similarly, since \(y \in \text{Int}(B)\) is an element of the interior of \(B\), there exists an open set \(V\) contained within \(Y\) such that \(y \in V \subseteq B\).

The product \(U \times V\) is an open set in the topological product \(X \times Y\) and contains the pair \((x, y)\).

Since \(U \times V\) is contained within \(A \times B\), this proves that \((x, y)\) belongs to \(\text{Int}(A \times B)\).

Thus, we have shown that \(\text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B)\).

2] The Product of the Interiors Contains the Interior of the Cartesian Product

Next, we need to prove that

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$

In other words, we need to show that if \((x, y) \in \text{Int}(A \times B)\), then \(x \in \text{Int}(A)\) and \(y \in \text{Int}(B)\).

Consider a pair of points \((x, y)\) belonging to \(\text{Int}(A \times B)\).

This implies that there exists an open set \(W\) within \(X \times Y\) such that \((x, y) \in W \subseteq A \times B\).

In the topological product, we can find open sets \(U\) and \(V\) in \(X\) and \(Y\) respectively, such that \(W\) contains a Cartesian product \(U \times V\) with \((x, y) \in U \times V \subseteq W\).

Since \(U \times V \subseteq A \times B\), we can deduce that \(U\) is contained within \(A\) and \(V\) is contained within \(B\).

This means that \(x \in U \subseteq A\) and \(y \in V \subseteq B\), so \(x\) belongs to the interior of \(A\) and \(y\) belongs to the interior of \(B\).

Therefore, \((x, y) \in \text{Int}(A) \times \text{Int}(B)\), which demonstrates that \(\text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B)\).

3] Conclusion

We have now demonstrated both inclusions:

$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$

$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$

Thus, we can conclude that the interior of the Cartesian product \(A \times B\) is equal to the product of the interiors of \(A\) and \(B\).

$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$

And with that, the theorem is confirmed.