Fixed Points in Topology

In topology, a fixed point refers to a value that remains constant under the application of a function.

Put simply, if you have a function f(x), a fixed point p is one where f(p) = p. This means the function's output matches its input when p is used.

$$ f(p) = p $$

Imagine rotating an object around a central point P.

Such a rotation maps the coordinates of the object's points in space.

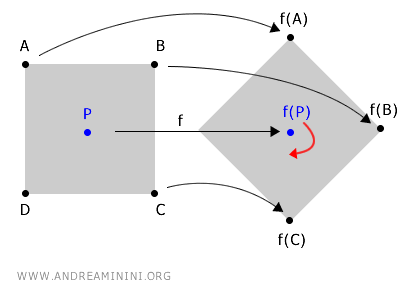
the rotation of the shape

In this scenario, the center of rotation, P, serves as a fixed point because its coordinates remain unchanged by the rotation function f(P).

$$ f(P) \longrightarrow P $$

Fixed points play a pivotal role across various mathematical fields and applications, such as numerical analysis, game theory, and economics.

A notable example from topology is the Brouwer Fixed Point Theorem.

A Practical Example

Consider the function f(x) = sin(x) across the closed interval [0, 2π] radians.

$$ f(x) = \sin(x) $$

The function's fixed point at p=0 radians is straightforward because sin(0) = 0.

$$ \sin(0) = 0 $$

Here, the output directly mirrors the input.

Example 2

Now take the function f(x) = cos(x) across the same interval [0, 2π] radians.

$$ f(x) = \cos(x) $$

This time, x=0 is not a fixed point as cos(0) = 1, indicating a mismatch between input and output.

The fixed point for the function f(x) = cos(x) occurs approximately at x = 0.73908513

$$ \cos(0.73908513) = 0.73908513 $$

Thus, cos(0.73908513) closely approximates 0.73908513.

This theorem declares:

Every continuous function mapping a closed n-dimensional interval guarantees at least one fixed point.

It's an existence theorem, highlighting the assurance of at least one fixed point without pinpointing its exact location.

This concept has broad implications, particularly in demonstrating the existence of equilibrium states in dynamic systems and economic models.

And so on.