Topological Graph
A topological graph is a topological space formed by taking a finite set of points, known as 'vertices', and a finite set of mutually disjoint closed intervals in \(\mathbb{R}\), called 'edges'. These edges are then connected to the vertices according to specific rules.
The topology of this space is defined by the way these connections are made, giving the topological graph a dual representation: both geometric and topological, showcasing the network of connections between the vertices.
This process results in a new space that embodies the structure of a graph.
Note. This is a type of quotient topology because it involves applying a topology to one space in order to create a new "induced" space. The new space is constructed by attaching a set of intervals to a set of vertices. In simpler terms, we take basic spaces (like closed intervals) and modify them by gluing them to certain points, resulting in a more complex topological space.
How to Construct a Topological Graph
Building a topological graph is a mathematical process that can be broken down into two main steps:
- Vertices: Start with a finite set of points, known as vertices. For example, these vertices could be labeled as A, B, C, D, E, and F.
- Edges: Then, consider a set of intervals (lines), each with two endpoints. These endpoints are "attached" (or connected) to specific vertices, creating links. These links, or intervals, are referred to as edges.
Essentially, this process involves taking lines (intervals) and connecting them to points (vertices) to form a structure called a graph.
It's called a "topological" graph because it is derived from the way spaces are connected or attached together.
A Practical Example
Let's take 3 distinct closed intervals in \(\mathbb{R}\):
$$ I_1 = [0, 1], \quad I_2 = [0, 1], \quad I_3 = [0, 1] $$
These are simple line segments, each having endpoints at \(0\) and \(1\).
Now, we define a set $ G $ consisting of 3 vertices, which we’ll label as \(A\), \(B\), and \(C\):
$$ G = \{ A, B, C \} $$
The vertices are just points to which we can attach the endpoints of the intervals.
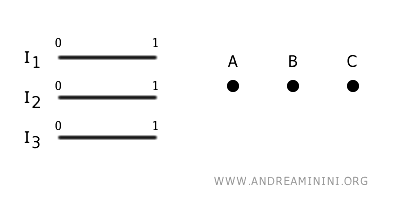
Next, we apply the quotient topology operation by attaching the endpoints of the intervals to specific vertices:
- Attach the endpoint \(0\) of interval \(I_1\) to vertex \(A\) and the endpoint \(1\) of \(I_1\) to vertex \(B\).
- Attach the endpoint \(0\) of interval \(I_2\) to vertex \(B\) and the endpoint \(1\) of \(I_2\) to vertex \(C\).
- Attach the endpoint \(0\) of interval \(I_3\) to vertex \(A\) and the endpoint \(1\) of \(I_3\) to vertex \(C\).
The result is a graph with 3 vertices \(A\), \(B\), and \(C\) and 3 edges: $ (A, B) $, $ (B, C) $, and $ (A, C) $.
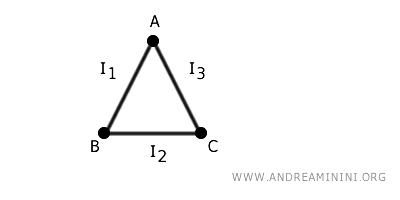
In this way, we've constructed a new structure (the topological graph) by starting with separate intervals and attaching their endpoints to vertices.
Essentially, creating the graph involves "wrapping" the intervals around the vertices.
And this process can continue further.
