Continuity in Topology

Let $X$ and $Y$ be two topological spaces. A function $f: X \to Y$ is considered continuous if, for every open set $V$ in $Y$, the preimage $f^{-1}(V)$ is an open set in $X$.

In other words, a continuous function in topology "preserves" the structure of open sets when it maps points from one space to another.

Continuity in topology is about maintaining the "consistency" of open sets between different spaces.

Note: Continuity in topology is a more general concept than continuity in mathematical analysis, which is based on the distance between points. In analysis, continuity involves the closeness of points; in topology, it focuses on how a function interacts with the structure of open sets. Essentially, the topological definition lets us determine if a function "respects" the structure of open sets, even in cases where the notion of distance does not apply.

For example, "stretching" or "deforming" a geometric shape without tearing it can be described by a continuous function.

Continuity ensures that the original structure (such as open sets) remains intact after the transformation.

A Practical Example
The basis theorem for continuity
Continuity in Coarse and Fine Topologies
Notes

A Practical Example

Consider two topological spaces $X = \{a, b, c, d\}$ and $Y = \{1, 2\}$.

In the space $X$, the open sets are: $\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}$.
In the space $Y$, the open sets are: $\{\}, \{1\}, \{1, 2\}$.

Now, let's define a function $f: X \rightarrow Y$ that maps these two spaces:

$ f(a) = 1 $, $ f(b) = 1 $, $ f(c) = 2 $, $ f(d) = 2 $

Is this function continuous according to the topological definition?

To illustrate this, we represent the function $f$ and the two topological spaces, highlighting the open sets in each space.

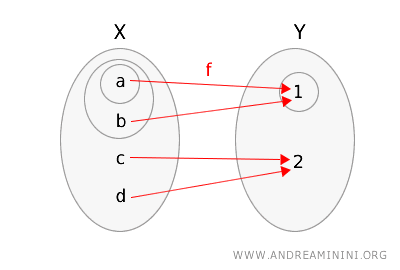
an example

Now, let's check if the definition of topological continuity is satisfied:

Consider the open set $\{1\}$ in $Y$; its preimage in $X$ is $ f^{-1}(\{1\}) = \{a, b\} $. This set $\{a, b\}$ is open in $X$.
Consider the open set $\{1, 2\}$ in $Y$; its preimage is $ f^{-1}(\{1, 2\}) = \{a, b, c, d\} $. This is also an open set in $X$.

We can skip verifying the empty set since it is open in every topology.

In conclusion, since the preimage of every open set in $Y$ is also open in $X$, the function $ f $ is continuous.

Example 2

Let's consider a different function $g: X \rightarrow Y$ between the same topological spaces:

$ g(a) = 1 $, $ g(b) = 2 $, $ g(c) = 2 $, $ g(d) = 2 $

We represent the function $g$ and the two topological spaces, highlighting the open sets.

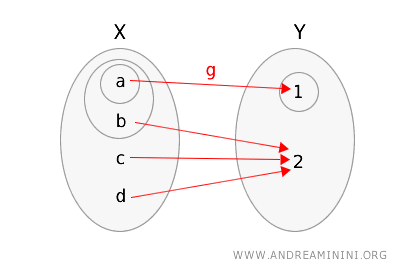
example

Finally, let's verify if the definition of topological continuity is satisfied:

Consider the open set $\{1\}$ in $Y$; its preimage in $X$ is $ g^{-1}(\{1\}) = \{a\} $. This set is open in $X$.
Consider the open set $\{2\}$ in $Y$; its preimage in $X$ is $ g^{-1}(\{2\}) = \{b, c, d\} $. This set is not open in $X$.

Since there is at least one open set in $Y$ whose preimage is not open in $X$, we can conclude that the function $g$ is not continuous.

Example 2

In this example, let's consider a simple identity function $ id: X \to X $ defined as $ id(x) = x $ for every $ x \in X $.

$$ x = f(x) $$

Essentially, the identity function doesn’t "change" anything. In topological terms, this means that the image of an open set in $ X $ remains an open set in $ X $.

Therefore, the identity function $ f(x) = x $ is always continuous because applying the identity function doesn’t alter the topological space $ X $.

Example 3

Now, let's look at a constant function $ f: X \to Y $ defined as $ f(x) = c $ for every $ x \in X $.

$$ f(x) = c $$

In other words, regardless of which element $ x $ in $ X $ we choose, the constant function "ignores" $ x $ and always returns the same value $ c $.

The definition of continuity in topology requires that for every open set $ V $ in $ Y $, the preimage $ f^{-1}(V) $ must also be an open set in $ X $.

There are two possible scenarios here:

If $ c $ belongs to $ V $ (meaning the fixed element we chose is within the open set $ V $), then the preimage of $ V $ under $ f $ is the entire space $ X $ because $ f(x) = c $ for all $ x $. Since the entire space $ X $ is open, $ f^{-1}(V) = X $ is also open.
If $ c $ does not belong to $ V $ (meaning the fixed element is outside of $ V $), then the preimage of $ V $ under $ f $ is the empty set ($ \emptyset $), which is also considered open.

In both scenarios, the preimage $ f^{-1}(V) $ is an open set in $ X $.

Thus, the constant function $ f(x) = c $ is continuous.

Note. This example emphasizes that the continuity of a function in topology depends not only on the "formula" of the function itself but also on the topological structures of the spaces involved. For the constant function, the preimage of any open set in $ Y $ is always an open set in $ X $, which is why the function is continuous.

Example 3

Let's once again consider the identity function $ f : X \to Y $, where $ f(x)=x $, but this time between two different topological spaces:

$ X $ is the space of real numbers $ \mathbb{R} $ with the standard topology, where open sets are intervals of the form $ (a,b) $, since every point in an open set must have a neighborhood that lies entirely within the set.
$ Y $ is the space of real numbers $ \mathbb{R} $ with the lower limit topology, where open sets are intervals of the form $[a, b)$.

To determine if the function $ f $ is continuous, we need to check whether the preimage of an open set in $ Y $ is also open in $ X $.

Consider a typical open set in $ Y $, such as $ [0, 1) $. This set is open in the lower limit topology.

The preimage of $ [0, 1) $ under $ f $ is simply $ [0, 1) $, because $ f $ is the identity function, so $ f^{-1}([0, 1)) = [0, 1) $.

However, in the standard topology, the interval $ [0, 1) $ is not an open set.

Note: In the standard topology, a set is open if, for every point in the set, there exists an open interval around that point which is fully contained within the set. In the case of $ [0, 1) $, the point $ 0 $ does not have a neighborhood around it that stays entirely within $ [0, 1) $, since any neighborhood around $ 0 $ would include negative numbers, which are not part of $ [0, 1) $.

Therefore, the identity function $ f : \mathbb{R} \to \mathbb{R} $, where $ \mathbb{R} $ has the standard topology in the domain and the lower limit topology in the codomain, is not continuous.

This is because there are open sets in $ Y $ (such as $ [0, 1) $) whose preimages are not open in the standard topology.

This example highlights that continuity in topology doesn't depend solely on the function itself but also on the topologies of the domain and codomain.

Even though the identity function $ f(x) = x $ is the same as in the first example, it is not continuous in this case.

The basis theorem for continuity

Given two topological spaces $ X $ and $ Y $, a function $ f: X \to Y $ is continuous if and only if, for every basis set $ B_Y $ of the topology on $ Y $, the preimage $ f^{-1}(B_Y) $ is an open set in $ X $.

This theorem is especially useful because it simplifies the process of verifying the continuity of a function.

Instead of checking the preimage of every open set in $ Y $, you only need to check the preimage of a much smaller collection of sets: those that form a basis for the topology on $ Y $.

This drastically reduces the number of checks required, making it much faster to verify continuity.

Proof. Every open set in $ Y $ can be written as a union of sets from its basis $ B_Y $. Therefore, if the preimage of each set in the basis $ B_Y $ is open in $ X $, it follows that the preimage of all open sets in $ Y $ will also be open in $ X $, since these open sets are unions of basis sets. This ensures that the condition for continuity is met, and thus the function $ f: X \to Y $ is continuous.

Example

Consider two topological spaces $ X = \{a, b, c, d\} $ and $ Y = \{x, y, z\} $, with the following topologies:

The topology on $ X $ is: $ \tau_X = \{\emptyset, \{a\}, \{a, b\}, \{a, b, c, d\} \} $.
The topology on $ Y $ has the basis $ B_Y = \{\{x\}, \{y\}, \{z\}\} $.

In this case, the full topology on $ Y $ is generated by unions of the basis elements. This allows us to construct many open sets that are not individual elements of the basis, but unions of them.

For example, the sets $ \{x, y\} $, $ \{x, z\} $, $ \{y, z\} $, and $ \{x, y, z\} $ are not part of the basis $ B_Y $, but they are still open sets in the space $ Y $ because they are formed by unions of the basis sets.

A function $ f: X \to Y $ is defined as follows:

$ f(a) = x $
$ f(b) = x $
$ f(c) = y $
$ f(d) = z $

To check if the function is continuous, we need to determine if the preimages of the basis sets $ B_Y = \{\{x\}, \{y\}, \{z\}\} $ of the topology on $ Y $ are open in $ X $.

$ f^{-1}(\{x\}) = \{a, b\} $, which is an open set in $ X $.
$ f^{-1}(\{y\}) = \{c\} $, which is not an open set in $ X $, as it is not part of the topology $ \tau_X $ (in other words, $ \{c\} $ is missing from the topology on $ X $).

Since the preimage of $ \{y\} $ is not open in $ X $, we can conclude that the function $ f $ is not continuous, as it fails the condition that the preimage of every basis set in $ Y $ must be open in $ X $.

Note. When the preimage of a basis set in $ Y $ is not open in $ X $, there is no need to check further preimages. Once we know that the preimage $ f^{-1}(\{y\}) = \{c\} $ is not open, it becomes unnecessary to check whether the preimage of $ \{z\} $ is open. It is sufficient for just one preimage of a basis set in $ Y $ to not be open in $ X $ to conclude that the function is not continuous.

Continuity in Coarse and Fine Topologies

If a function is continuous with respect to the coarser topology, it will also be continuous with respect to the finer topology.

However, the reverse is not always true: a function can be continuous in the finer topology but fail to be continuous in the coarser one.

Difference between finer and coarser topology. Given two topologies on the same set $ X $, one is called "coarser" than the other if it has fewer open sets. Conversely, it is called "finer" if it has more open sets.

Example

Let’s consider the set $ X = \{a, b\} $ with two topologies:

Coarser topology $ \tau_1 = \{\varnothing, \{a, b\}\} $, where only the empty set and the entire set $ \{a, b\} $ are open.
Finer topology $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $, where the subsets $ \{a\} $ and $ \{b\} $ are also open, in addition to the whole set.

Now, let’s define a function $ f: X \to Y $, where $ Y = \{1\} $, as follows:

$$ f(a) = 1 $$

$$ f(b) = 1 $$

In the coarser topology $ \tau_1 $, the open sets are $ \varnothing $ and $ \{a, b\} $.

Let’s verify the continuity of $ f $:

$ f^{-1}(\varnothing) = \varnothing $ is the empty set, which by definition is open in $ \tau_1 $
$ f^{-1}(\{1\}) = \{a, b\} $, which is also open in $ \tau_1 $

Since $ \{a, b\} $ is open in $ \tau_1 $, the function $ f $ is continuous with respect to the coarser topology $ \tau_1 $.

Because the preimages remain the same, the function $ f $ must also be continuous with respect to the finer topology $ \tau_2 $.

In the finer topology $ \tau_2 $, the open sets are $ \varnothing $, $ \{a\} $, $ \{b\} $ and $ \{a, b\} $.

$ f^{-1}(\varnothing) = \varnothing $ is open in $ \tau_2 $
$ f^{-1}(\{1\}) = \{a, b\} $, which is also open in $ \tau_2 $

Since $ \{a, b\} $ is open in $ \tau_2 $, the function $ f $ is continuous with respect to the finer topology $ \tau_2 $ as well.

In conclusion, the function $ f $ is continuous in both the coarser and finer topologies, because the finer topology includes more open sets, but all open sets of the coarser topology are also open in the finer one.

However, the reverse is not always true. A function can be continuous in the finer topology but not in the coarser one, as the coarser topology has fewer open sets and thus fewer constraints on continuity.

Example 2

Let’s again consider the set $ X = \{a, b\} $ with the same topologies:

Coarser topology $ \tau_1 = \{\varnothing, \{a, b\}\} $
Finer topology $ \tau_2 = \{\varnothing, \{a\}, \{b\}, \{a, b\}\} $

Now, let’s define a function $ g: X \to Y $, where $ Y = \{1,2\} $, as follows:

$$ g(a) = 1 $$

$$ g(b) = 2 $$

The function $ g $ is continuous with respect to the finer topology $ \tau_2 $ because all the preimages of $ Y $ are open in $ \tau_2 $:

$ g^{-1}(\varnothing) = \varnothing $, which is open in $ \tau_2 $
$ g^{-1}( \{1,2 \} ) = \{a,b\} $, which is open in $ \tau_2 $
$ g^{-1}( \{1 \} ) = \{a\} $, which is open in $ \tau_2 $
$ g^{-1}( \{2 \} ) = \{b\} $, which is open in $ \tau_2 $

However, the function $ g $ is not continuous with respect to the coarser topology $ \tau_1 $ because some of the preimages of $ Y $ are not open in $ \tau_1 $:

$ g^{-1}(\varnothing) = \varnothing $, which is open in $ \tau_1 $
$ g^{-1}( \{1,2 \} ) = \{a,b\} $, which is open in $ \tau_1 $
$ g^{-1}( \{1 \} ) = \{a\} $, which is not open in $ \tau_1 $

In conclusion, the function $ g $ is continuous with respect to the finer topology $ \tau_2 $, but it is not continuous with respect to the coarser topology $ \tau_1 $.

Notes

Some side notes on topological continuity.

A continuous function is not necessarily an open map
A continuous function doesn't always map open sets to open sets. Therefore, continuity doesn't imply that open sets are preserved, unlike with open maps.
Pasting Lemma
Given two continuous functions, $ f: A \to Y $ and $ g: B \to Y $, defined on two overlapping sets $ A $ and $ B $ that agree on their intersection, they can be 'combined' to create a new continuous function $ h $, defined on the union $ A \cup B $ of the two sets.
Continuity in the subspace topology
Given a topological space $ X $ and a subset $ Y $, the inclusion function $ f $ maps each point in $ Y $ to the same point in $ X $ (in other words, $ f(y) = y $ for all $ y \in Y $). This function is continuous.
Continuity in the quotient topology
When we have a surjective function $ f $ from a topological space $ X $ to a set $ A $, the quotient topology on $ A $ is defined so that $ f $ remains continuous. The quotient topology is specifically constructed to ensure $ f $ is continuous.
Theorem on the continuity of closure
Continuity preserves the property of a point being part of the closure of a set. If a point $ x \in X $ is in the closure of a set $ A \subset X $ (i.e., $ x \in Cl(A) $), then its image $ f(x) $ will also be in the closure of the image of $ A $, meaning $ f(x) \in Cl(f(A)) $.
Continuity defined by open sets
A function is continuous if and only if, for every open set $ U \subset Y $, the preimage $ f^{-1}(U) $ is an open set in $ X $.
Continuity defined by closed sets
The function $ f : X \to Y $ is continuous if and only if, for every closed set $ C \subset Y $, the preimage $ f^{-1}(C) $ is a closed set in $ X $.
Theorem on the composition of continuous functions
If two functions $ f $ and $ g $ are continuous, then the composition $ g \circ f $ is also continuous.
Continuity and converging sequences
The theorem states that if a function $ f: X \to Y $ is continuous, and a sequence of points $ x_1, x_2, \dots $ in $ X $ converges to a point $ x $, then the sequence of the corresponding values $ f(x_1), f(x_2), \dots $ will converge to $ f(x) $ in $ Y $.
Polynomial functions
In the topological space $\mathbb{R}$ with the standard topology, any polynomial function $p : \mathbb{R} \to \mathbb{R}$, where $p(x) = a_nx^n + \dots + a_1x + a_0$, is continuous.

And so on.