Continuity Definition Using Open Sets

A function $ f : X \to Y $ is continuous if and only if, for every point $ x \in X $ and every open set $ U \subset Y $ containing $ f(x) $, there exists a neighborhood $ V $ of $ x $ such that $ f(V) \subset U $.

In simpler terms, a function $ f: X \to Y $ is continuous if, for every open set $ U \subset Y $, the preimage $ f^{-1}(U) $ is an open set in $ X $.

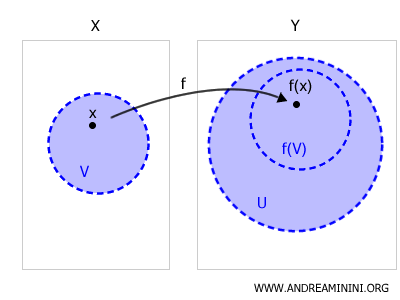
example

Continuity means that the preimage of any open set in the codomain is always an open set in the domain.

This theorem provides a topological definition of continuity, relying on the concept of open sets in both the domain and codomain.

It's also referred to as the open set definition of continuity.

Note: This theorem is also known as the "equivalence of definitions of continuity" because it shows that the two ways to define continuity for a function—the one with open sets (topological) and the analytical one with $\varepsilon$-$\delta$—are equivalent. The analytical definition of continuity is the following: "A function $ f $ is continuous at a point $ x_0 \in \mathbb{R} $ if, for every $\varepsilon > 0$, there exists a $\delta > 0$ such that for every $ x \in \mathbb{R} $, if $ |x - x_0| < \delta $, then $ |f(x) - f(x_0)| < \varepsilon $," which is commonly covered in introductory calculus courses.

The opposite is also true: continuity can equally be defined using closed sets.

Given two topological spaces $ X $ and $ Y $, a function $ f: X \to Y $ is continuous if and only if the preimage $ f^{-1}(C) $ of every closed set in $ Y $ is also a closed set in $ X $.

Thus, the concept of continuity can be described in terms of either open or closed sets, as the properties of openness and closedness are inherently linked in topology.

A Practical Example
Proof

A Practical Example

Consider the function $ f : \mathbb{R} \to \mathbb{R} $ defined as $ f(x) = x^2 $.

We want to determine whether this function is continuous using the open set definition from the theorem.

According to the open set definition of continuity:

A function $ f $ is continuous if, for every open set $ U \subset \mathbb{R} $ and for every $ x \in f^{-1}(U) $, there exists a neighborhood $ V $ of $ x $ such that $ f(V) \subset U $.

Let's choose an open set $ U \subset \mathbb{R} $.

For example, take the open set $ U = (1, 4) $, which includes all the numbers between 1 and 4.

open set example

We want to check if $ f^{-1}(U) $, the set of numbers in $ \mathbb{R} $ that are mapped into the interval $ (1, 4) $ by $ f(x) = x^2 $, is open.

To find $ f^{-1}(U) $, we need to determine which values of $ x $ satisfy $ x^2 \in (1, 4) $. In other words, we are looking for $ x $ such that:

$$ 1 < x^2 < 4 $$

This inequality leads to:

$$ 1 < |x| < 2 $$

Therefore, $ x $ must lie within the interval $ (-2, -1) \cup (1, 2) $.

This is the set $ f^{-1}(U) $, which is clearly an open set in $ \mathbb{R} $.

Now, let’s verify the continuity.

We select any point $ x \in f^{-1}(U) $, where $ U = (1, 4) $. For example, take $ x = 1.5 $.

The image of $ x = 1.5 $ is $ f(1.5) = 1.5^2 = 2.25 $, which is within the interval $ U = (1, 4) $.

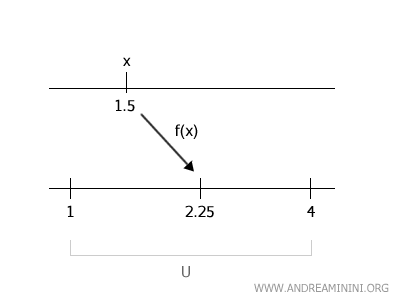
example

We now need to find a neighborhood $ V $ around $ x = 1.5 $ such that $ f(V) \subset (1, 4) $.

Let’s choose a small interval around $ 1.5 $, say $ V = (1.4, 1.6) $.

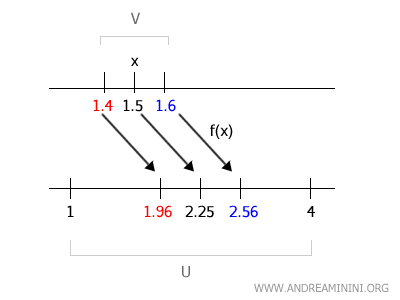
example

By calculating the values of $ f(x) = x^2 $ for $ x \in (1.4, 1.6) $, we get:

$$ f(1.4) = 1.4^2 = 1.96 \quad \text{and} \quad f(1.6) = 1.6^2 = 2.56 $$

The interval $ f(V) = (1.96, 2.56) $ is entirely contained within the open interval $ U = (1, 4) $.

$$ f(V) \subset U $$

This demonstrates that for every point $ x \in f^{-1}(U) $, there is a neighborhood $ V $ of $ x $ such that $ f(V) \subset U $, satisfying the definition of continuity.

The same holds for any other point $ x \in \mathbb{R} $, confirming that the function $ f(x) = x^2 $ is continuous according to the open set definition of continuity.

Note: Continuity must be verified for all points $ x \in X $. It’s not enough to check the condition at a single point. This is because the continuity of a function is a global property—it must hold at every point in the domain. To prove that a function $ f : \mathbb{R} \to \mathbb{R} $ is continuous, we need to show that for every point $ x \in \mathbb{R} $ and for every open set $ U $ containing $ f(x) $, there exists a neighborhood $ V $ of $ x $ such that $ f(V) \subset U $.

Proof

The proof is divided into two parts:

A] First Part

Assume the function $ f $ is continuous according to the open set definition.

We choose a point $ x \in X $ and an open set $ U \subset Y $ such that $ f(x) \in U $.

Now, we define $ V = f^{-1}(U) $, which is the set of all points in $ X $ that map into $ U $ under $ f $.

Since $ f $ is continuous by the open set definition, we know that $ V $ is an open set in $ X $.

Thus, because $ x \in V $ and $ f(V) \subset U $, we have shown that for every open set $ U $ in $ Y $ containing $ f(x) $, there is an open set $ V $ in $ X $ containing $ x $.

B] Second Part

Assume that for every point $ x \in X $ and for every open set $ U \subset Y $ containing $ f(x) $, there is a neighborhood $ V $ of $ x $ such that $ f(V) \subset U $.

We need to prove that $ f^{-1}(W) $ is open in $ X $ for every open set $ W \subset Y $.

In other words, we need to show that the set of points in $ X $ that are mapped into $ W $ by $ f $ is open.

We take a point $ x \in f^{-1}(W) $, meaning a point $ x $ in $ X $ such that $ f(x) \in W $.

Since $ f(x) \in W $ and $ W $ is open, by assumption, there exists a neighborhood $ V_x $ of $ x $ in $ X $ such that $ f(V_x) \subset W $.

This means that $ V_x \subset f^{-1}(W) $, so $ f^{-1}(W) $ contains an open neighborhood $ V_x $ around $ x $.

Because $ x $ was arbitrary, we can conclude that $ f^{-1}(W) $ is open in $ X $.

Conclusion

In conclusion, the two definitions of continuity—using open sets and using neighborhoods—are equivalent.

And so on.