Closure of a set

The closure of a set \( A \) within a topological space \( X \) is the intersection of all closed sets that contain \( A \). This intersection is denoted by \( \text{Cl}(A) \).

The closure of set A is the smallest closed set that completely encompasses A.

No closed set containing A is smaller than its closure.

Note: This observation directly follows from the definition of set closure, which is formed by intersecting all closed sets that contain A. Essentially, the closure is the tightest closed set around A, consisting of elements common to every closed set that includes A.

Formally, the closure of set A is represented as:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ and } C \text{ is closed in } X \} $$

Here, \( \text{Cl}(A) \) signifies the closure of \( A \), and the symbol \( \bigcap \) represents the intersection of all closed sets \( C \) that contain \( A \).

The closure of \( A \) includes both the set \( A \) itself and all its limit points within \( X \).

Note: It's crucial to understand that the closure of a set \( A \) is influenced more by the topology of the space \( X \) in which \( A \) resides, rather than by the intrinsic properties of \( A \) itself. Consequently, the closure of \( A \) may differ based on \( X \)'s specific topology.

An Illustrative Example

Consider the set \( A = (0, 1) \) within the real numbers \( \mathbb{R} \) under the standard topology.

This represents the open interval that includes all real numbers from 0 to 1, excluding the endpoints.

In this scenario, the closure of \( A \) is \( [0, 1] \).

$$ \text{Cl}(A) = [0,1] $$

This set incorporates the original open interval \( (0,1) \) along with its accumulation points at the boundaries, namely the points 0 and 1.

Note: Under the standard topology on \( \mathbb{R \), closed sets are those that include all their limit points. A limit point of a set is a point such that every neighborhood around it contains at least one distinct point of the set. For example, the intersection of the closed intervals [0,2] and [-1,1] results in the closed interval [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ No smaller closed interval can contain (0,1).

Example 2

Let's examine the set \( A = [0, 1) \) in \( \mathbb{R \) under standard topology.

This set encompasses all real numbers starting from 0, inclusive, up to 1, exclusive. It is therefore a left-closed and right-open interval.

Once again, the closure of the set is $ [0,1] $.

$$ \text{Cl}(A) = [0,1] $$

This occurs because the endpoint 0 is already included within the set A, while 1 is an external limit point.

Therefore, the closure of A incorporates the right open endpoint of the interval, rendering [0,1] the smallest closed set that contains A.

Note: This aligns with the closure concept in topology, which encompasses all accumulation points of a set. For example, the intersection of [0,2] and [-1,1] is [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$

Example 3

Now, let's analyze the same set \( A = [0,1) \) when \( X \) operates under the discrete topology.

In discrete topology, every subset of a topological space is deemed open and simultaneously closed.

• Open Set
  In a space with discrete topology, every subset of \( X \) is an open set. Since \( A \subset X \) is a subset of X, A is consequently an open set.
• Closed Set
  Similarly, every subset of \( X \) is also considered closed because its complement is an open set. For instance, the complement \( X/A \) is an open set because it is a subset of X, namely \( X/A \subset X \). Thus, the set A is closed because its complement X/A is open.

This indicates that every set is both open and closed, a concept known as a clopen set.

Consequently, the closure of a set \( A \) is merely \( A \) itself, as no additional points are necessary to "close" the set.

$$ \text{Cl}(A) = [0,1) $$

The smallest closed set that encompasses \( A \) is \( A \) itself.

Note: This result shows how the choice of topology can significantly influence the closure of sets. As previously stated, the properties of a closed set are not inherent to the set \( A \) itself but depend on the topological structure \( X \) within which \( A \) is defined.

Example 4

Consider a topological space \( X \) consisting of points \( \{a, b, c \} \), equipped with a discrete topology.

In discrete topology, every subset of \( X \) is open:

• \( \emptyset \) and \( \{a, b, c \} \) are open by definition.
• Each individual point \( \{a\} \), \( \{b\} \), \( \{c\} \) is considered an open set.
• Any possible combination of these open sets, such as \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \)  is also open.

Furthermore, in the discrete topology, every subset of \( X \) is also seen as closed, given that the complement of each subset is also an open set.

This means that in the discrete topology, every set is both open and closed.

When considering the set \( A = \{b, c\} \) within the topological space \( X \), it is open as it is a subset of X and every subset in the discrete topology is open. It is also closed because its complement \( X/A = \{ a \} \) is an open set.

The closure of \( A \), \( Cl(A) \), being the intersection of all closed sets that include \( A \), needs no additional elements to complete its closure.

Thus the closure of \( A \) is \( A \) itself:

\[ Cl(A) = \{b, c\} \]

In this topology, every set is both open and closed, thus no further "closure" is necessary, as it is already complete.

Note: For a quick verification, the closed sets that include \( A \) are \( \{b, c\} \) and \( \{a,b,c\} \). $$ Cl(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ The intersection of these sets is \( \{b, c\} \), exactly matching \( A \). Therefore, \( Cl(A) = A \).

The Closure Theorem of a Set

In a topological space \( X \), an element \( y \) belongs to the closure of a subset \( S \), denoted \( \text{Cl}(S) \), if and only if every open set \( U \) containing \( y \) intersects \( S \) non-trivially: \( y \in \text{Cl}(S) \iff \forall \ U \text{ open with } y \in U, \ U \cap S \neq \emptyset \).

In simpler terms, for an element \( y \) within \( X \) to be considered part of the closure of \( S \), it must also lie in an open set \( U \) that intersects with \( S \).

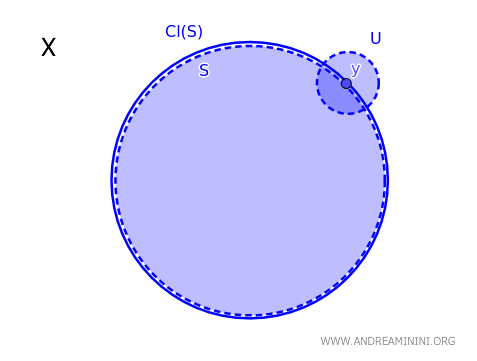
This theorem offers a valuable criterion to determine if a point is part of the closure of a set \( S \) in a topological space \( X \).

Proof

• Necessary condition: If \(y\) is found within the closure of \(S\), then by definition, every open set that includes \(y\) must intersect \(S\). This reflects the nature of closures, which encompass all of a set’s points, including its limit points. A limit point requires that any open neighborhood containing it must intersect the set from which it derives.
• Sufficient condition: Conversely, if every open set that contains \(y\) intersects \(S\), then \(y\) qualifies either as a limit point of \( S \) or as an actual point of \( S \). Hence, \(y\) invariably belongs to the closure of \(S\). This holds true because \(y\) can be approached infinitely closely by points within \(S\), implying that \(y\) is a limit point of \(S\) or is directly a part of \(S\).

Note: This theorem is frequently referenced in set topology as it bridges the concept of an open set with the closure properties of sets, which are fundamental in exploring continuity, sequence convergence, and other topological properties. It also plays a crucial role in the proof of various other theorems.

Example

Consider the set \( A = (0, 2) \) within the standard topology of \( \mathbb{R} \). Here, \( A \) is simply an open interval on the real numbers.

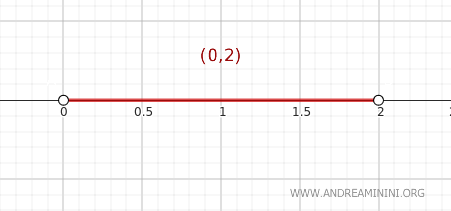
Applying the closure theorem to ascertain whether a point \( y \) belongs to \( \text{Cl}(A) \), the closure of set A:

Take, for example, the point \( y = 2 \) in \( \mathbb{R} \).

According to the theorem, \( y \) belongs to \( \text{Cl}(A) \) if and only if every open set \( U \) containing \( y \) intersects \( A \).

1. Examining open sets that include \( y \): Whenever I select an open set \( U \) that encompasses the point \( y = 2 \), such as \( (1.9, 2.1) \), \( (1.95, 2.05) \), \( (1.99, 2.01) \), etc., I find that these intervals invariably include points that are also part of the interval \( A = (0, 2) \). For instance, points like \( 1.95, 1.99 \) are all greater than 0 and less than 2.
2. Confirming the intersection of each \( U \) with \( A \): Since every open set \( U \) around \( y = 2 \) intersects \( A \), I can conclude under the theorem’s terms that \( y = 2 \) belongs to \( \text{Cl}(A) \).

Thus, the point \( y = 2 \) is within the closure of \( A \) because every open set that contains it intersects \( A \), fulfilling the theorem’s stipulations.

$$ y \in \text{Cl}(A) $$

Indeed, the closure of set \( A \) is the closed interval \( \text{Cl}(A) = [0, 2] \) which encompasses the point \( y = 2 \).

Closure Properties in Topological Spaces

This section explores various properties related to the closure of a set within a topological space, as well as some intriguing relationships between operations like taking the interior and closure of a set, which may not be immediately intuitive.

• Interior of the Complement and Complement of the Closure
  The interior of the complement of a set \( A \) is equal to the complement of the closure of \( A \). This relationship can be mathematically represented as: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
• Closure of the Complement and Complement of the Interior
  The closure of the complement of a set \( A \) is equal to the complement of the interior of \( A \). This formula is expressed as: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

Key Observations

Here are some notable insights, margin annotations and notes:

• If C is a closed set in X and A ⊆ C, then Cl(A) ⊆ C
  In a topological space \( X \), if \( C \) is a closed set and set \( A \) is contained within \( C \), the closure of \( A \), denoted \( \text{Cl}(A) \), must also be a subset of \( C \). This is because the closure of \( A \) is the smallest closed set that encompasses \( A \), and since \( C \) already includes \( A \) and is closed, it naturally contains \( \text{Cl}(A) \) as well. Thus, \( \text{Cl}(A) \) cannot extend beyond the boundaries of \( C \).
• If A ⊆ B, then Cl(A) ⊆ Cl(B)
  If set \( A \) is included in another set \( B \), then the closure of \( A \) (composed of \( A \) and all its limit points) will invariably be a subset of the closure of \( B \). This is because the limit points of \( A \) are also limit points for \( B \), as \( B \) encompasses \( A \). Hence, the closure, which is the intersection of all closed sets containing the original set, must comply with this inclusion principle.
• A set A is closed if and only if A equals Cl(A)
  In topological terms, a set \( A \) is considered closed if it is equivalent to its closure, meaning \( A = \text{Cl}(A) \). The closure of \( A \), \( \text{Cl}(A) \), incorporates all points in \( A \) plus its limit points. Therefore, if \( A \) contains all its limit points, it qualifies as closed.
• The closure of a set equals the union of the set and its limit points
  For a set A and its set of limit points A', the closure of A is the union of A and A'. $$ \text{Cl}(A) = A \cup A' $$
• Idempotence
  Once a set is closed, further closure doesn't introduce new points. $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
• Invariance with respect to the set
  The original set is always contained in its closure. $$ A \subseteq \text{Cl}(A) $$

More to follow.