Closed Sets
A set B within a topological space X is considered a closed set if, for every element in the complement set u∈X-B, there exists a neighborhood that still belongs to the complement set X-B.
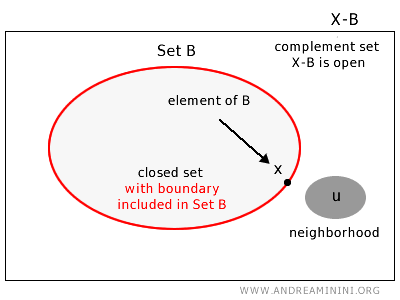
In simpler terms, a set is closed if its "boundaries" are elements that belong to the set itself.
To put it more formally, a set B in a topological space X is deemed closed if its complement set X-B is an open set.
Note: This implies that there is at least one element within the closed set B around which a neighborhood entirely contained within B cannot be found.
A Practical Example
Consider the real number line R and any closed interval.
What is a closed interval? A closed interval on R is defined as the set of all points x such that a≤x≤b, where a and b are real numbers with $ a \lt b $, and both are included in the interval.
Closed intervals are denoted by [a,b], where the square brackets indicate that the endpoints a and b are included in the set.
For example, the closed interval [3,10] is a closed set on the real number line R.
In this case, set B consists of an infinite number of numbers between 3 and 10, inclusive.
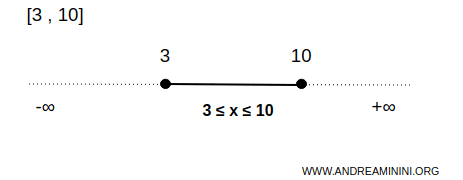
This means all points x satisfying the condition 3≤x≤10 are included in the set, including the endpoints 3 and 10.
In this instance, not all elements have a neighborhood entirely contained within the interval [3,10].
For instance, any neighborhood of the lower endpoint x=3 is not entirely contained within the interval [3,10].
Note: Even if one were to consider an infinitesimal neighborhood, such as 3±0.00000001, it would not be included in the closed interval [3,10] because 3-0.00000001 is less than 3. The same applies to the upper endpoint x=10. Here too, there is no neighborhood entirely contained within the interval [3,10].
This is a simple one-dimensional example of a closed set.
Other Examples of Closed Sets
The same example can be extended to two-dimensional space, or the plane.
For example, the set of points of a circle with radius r=1 and center at the origin (0,0).
$$ x^2+y^2≤1 $$
This inequality describes the set of all points whose distance from the center (0,0) is less than or equal to 1, thus including both the points on the circumference and those inside the circle.
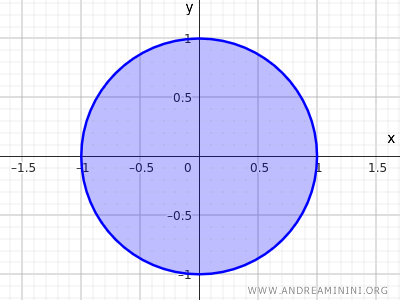
This is another example of a closed set.
As can be easily understood, the points on the circumference do not have a neighborhood entirely included in the set.
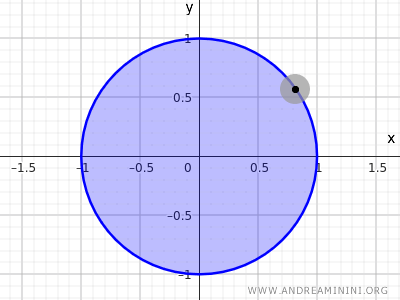
Note: In topology, the circle defined by the equation $ x^2+y^2=1 $ is neither an open nor closed set in Euclidean space R2, as it only considers the points on the circumference, excluding the interior. Conversely, the set of points defined by the inequality $ x^2+y^2≤1 $, which includes both the internal points and those on the circumference, is an example of a closed set because it includes all its boundary points (the circumference).
Following the same logic, the concept of a closed set can be extended to three-dimensional space through a sphere, and to n-dimensional space with an n-dimensional sphere.
The Complement of a Closed Set
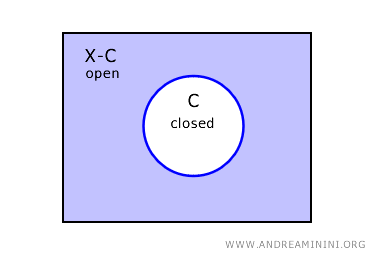
In space X, the complement of a closed set C is an open set, denoted as X-C.
If set C is closed within space X, its complement, X-C, will inherently be an open set.
Conversely, if a set U is open, its complement, X-C, becomes a closed set in space X.
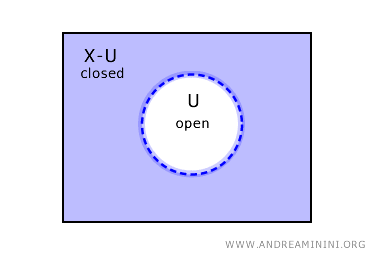
These are not the sole scenarios, however. Topological spaces may also feature sets that are both closed and open as well as sets that are neither open nor closed.
Simply put, the absence of closure does not imply openness, and lacking openness does not necessarily infer closure.
Example
Consider, for example, topology T on set X={a,b,c,d}, which includes four elements.
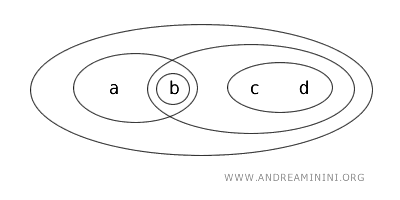
Under topology T, the following sets are classified as "open": {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.
Let's take a closer look at these sets:
- {b} is an open set, as designated by the topology itself.
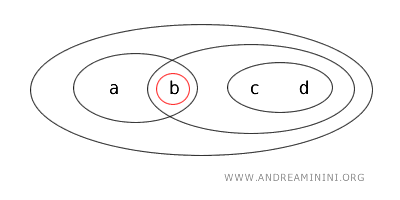
- {a} is a closed set because it forms the complement of the open set X-{b,c,d}={a}, where X={a,b,c,d}.
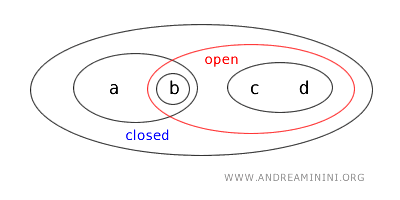
- {a, b} is both open and closed, an unusual occurrence known as "clopen". While rare in standard topologies on ℝ, such cases are possible in general topological spaces when the defined open sets include a set and its complement. Here, {a,b} is open as per topology T's designation and closed because it is the complement of the open set X-{c,d}.
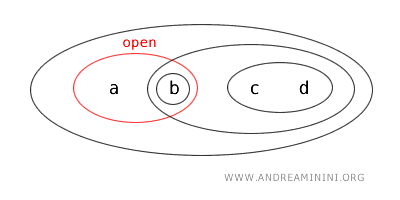
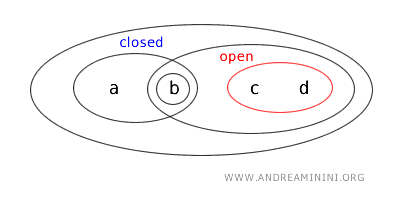
- {b, c} is neither open nor closed. It fails to meet the open set criteria and is not a complement of any open set. It is undefined as "open" by the topology and lacks the characteristics of a closed set, making {b,c} neither open nor closed.
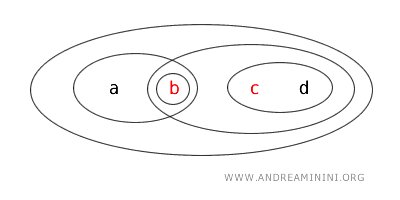
This example underscores that within a topology, sets can be open, closed, both, or neither.
Properties of a Closed Set
A closed set is defined as the complement of an open set. It exhibits the following key properties:
- The empty set (denoted as Ø) and the entire space (X) are inherently considered closed.
- The intersection of any number of closed sets is also a closed set.
- The union of a finite number of closed sets remains a closed set.
Example:
For example, in the standard topology of Euclidean space Rn, every single point is a closed set
For a single point n on a line (R1), the complement is all points on R1 that are not n.
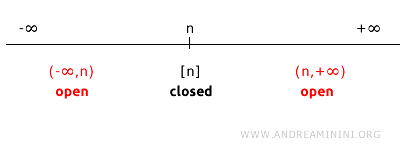
Hence, the complement of {n} is the union of two open intervals: (-∞, n) ∪ (n, +∞).
As these intervals (-∞, n) and (n, +∞) are open in standard topology, their union (-∞, n) ∪ (n, +∞) is also an open set.
Since the complement of {n} is an open set, we deduce that {n} is indeed a closed set.
It should be noted, however, that not every single point is automatically a closed set; this depends on the topology of the space. For example, in a different topology on R (the real number line), single points may not be closed sets. Consider a topology on R generated using the open intervals (n, n + 1) for every integer n. In this topology, individual points (n) are not closed because they exclude the boundaries around them.
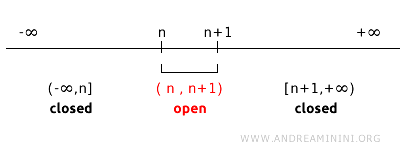
For instance, in this topology, the sets (1,2) and (2,3) are considered open. The complement of the open set (1,2) is the set (-∞, 1]∪ [2, +∞), whereas the complement of the open set (2,3) is the set (-∞, 2]∪ [3, +∞). Therefore, it is impossible to find a complement matching the closed set [2] in this topology. Generally, for any open set (n, n+1), its complement is the union of closed sets (-∞, n]∪ [n+1, +∞). Consequently, in this topology, individual points n are not regarded as closed sets, demonstrating that the definition of a closed set is contingent upon the topology applied.
Footnotes
Some observations and side notes
- Closed Sets and Their Limit Points
A limit point of a set is a point around which every neighborhood, no matter how small, contains at least one other point from the set. This characteristic defines closed sets, as they include all their limit points, whereas open sets might not.Example: Take the closed interval [0, 1] on the real axis. This interval includes all its limit points. Consider a point like 0.5 within [0, 1]. Around this point, there exists an open neighborhood that encompasses countless other points within [0, 1], confirming that 0.5 is indeed a limit point.
![example of 0.5 as a limit point in the closed interval [0,1]](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
This holds true for all points in [0, 1], including the boundary points. For example, the endpoint 0 of the interval is a limit point because nearby points like 0.1, 0.01, 0.001, and so forth, are all within the interval.
![the endpoints of the closed interval [0,1] are limit points](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
Thus, every point in the closed interval [0, 1] is surrounded by open neighborhoods filled with additional points from the interval. - A set A is closed if and only if A = Cl(A)
In a topological space, a set \( A \) is considered closed if it is equal to its closure, meaning \( A = \text{Cl}(A) \). The closure of \( A \), \( \text{Cl}(A) \), encompasses all the points of \( A \) as well as all its limit points. By definition, if a set \( A \) contains all its limit points, then it is a closed set.
And so on.
