Homeomorphisms in Topology
A homeomorphism is defined as a transformation within topology that involves a bijective and continuous function along with its continuous inverse.
Essentially, this allows one space to be transformed into another and back again without any "breaking" or "gluing."
In simpler terms, a homeomorphism lets you morph one space into another seamlessly, without tearing or attaching anything.
Take, for example, a coffee mug with a handle and a doughnut (torus) - these are considered homeomorphic in topology. This is because one can be continuously deformed into the other, and vice versa.

In topological terms, these are equivalent shapes as both feature a single "hole" - the doughnut's central hole and the mug's handle gap. You could mold the mug around its handle to shape it into a doughnut.
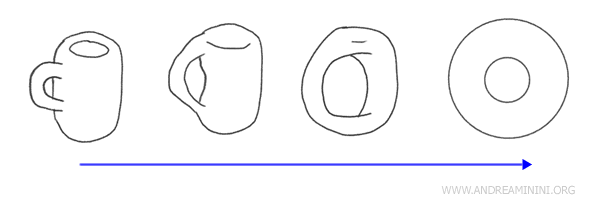
When two topological spaces are connected by a homeomorphism, they are referred to as "homeomorphic spaces," indicating that, topologically, they are fundamentally the same, even if their geometric appearances are distinct.
Characteristics of a Homeomorphism
The following are key features of a homeomorphism:
- Bijective function
It establishes a one-to-one correspondence between the elements of two spaces, ensuring that each element of one space matches exactly one element of the other, and vice versa. - Continuity
A homeomorphism is inherently continuous, meaning minor changes in input result in minor changes in output. - Continuous inverse function
The inverse function of a homeomorphism also needs to be continuous, allowing the transformation to be reversible while maintaining continuity. - Preservation of topological properties
It maintains the intrinsic topological properties such as continuity, connectedness, and compactness. Thus, relationships within the original space are preserved in the transformed space.
A homeomorphism is, essentially, a continuous and invertible function between two topological spaces \(X\) and \(Y\), where the inverse function is also continuous. This preserves the topological properties of both spaces.
Simply put, a homeomorphism is a way to "reshape" one space into another without tearing or merging parts together. It's a kind of "perfect match" between two shapes or spaces.
It's important to recall the definition of continuity in topology:
Given two topological spaces \(X\) and \(Y\), a function \(f: X \to Y\) is said to be continuous if, for every open set \(V\) in \(Y\), the preimage \(f^{-1}(V)\) is an open set in \(X\).
In other words, a continuous function in topology "preserves" the structure of open sets when mapping points from one set to another.
Therefore, continuity in topology is a more flexible and abstract version of the concept of continuity used in mathematical analysis.
Note: In mathematical analysis, continuity is based on the distance between points. In topology, however, it relies on the structure of open sets, which is more general and doesn't require a notion of distance.
A Practical Example
Let’s try to illustrate the concept of homeomorphism and continuity using open sets in a straightforward way.
Consider two topological spaces \(X = \{a, b, c, d\}\) and \(Y = \{1, 2\}\).
- In the space \(X\), the open sets are: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
- In the space \(Y\), the open sets are: \(\{\}, \{1\}, \{1, 2\}\).
A function \(f: X \rightarrow Y\) is continuous if, for every open set in \(Y\), the preimage is an open set in \(X\).
Now, let's define a function \(f: X \rightarrow Y\) as follows:
\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).
For simplicity, I will represent the function \(f\) and the two topological spaces by circling the open sets.
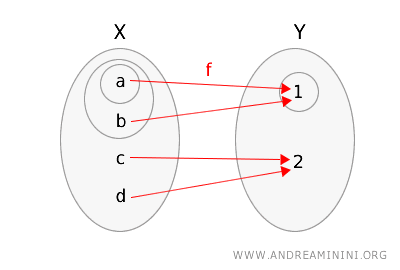
Let's verify whether it satisfies the definition of topological continuity.
- If we take the open set \(\{1\}\) in \(Y\), the preimage in \(X\) is \(f^{-1}(\{1\}) = \{a, b\}\). This set \(\{a, b\}\) is open in \(X\).
- If we take the open set \(\{1, 2\}\) in \(Y\), the preimage is \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\). This is also an open set in \(X\).
Since the preimage of every open set in \(Y\) is an open set in \(X\), this function is continuous.
Note: I have excluded the empty set since it is, by definition, open in any topological space.
Now, let's see what happens if we consider a different function \(g: X \rightarrow Y\) defined as:
\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).
Again, I will represent the function \(g\) and the two topological spaces by circling the open sets.
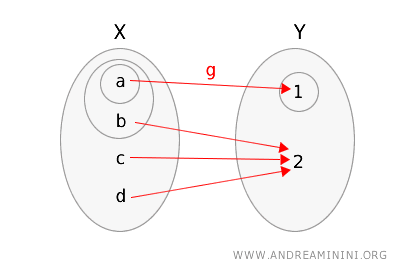
Let's check if this satisfies the definition of topological continuity.
- If we take the open set \(\{1\}\) in \(Y\), the preimage in \(X\) is \(g^{-1}(\{1\}) = \{a, b, c\}\). This set is not open in \(X\).
Since there is at least one open set in \(Y\) (in this case, \(\{1\}\)) whose preimage is not open in \(X\), the function \(g\) is not continuous.
Note: In conclusion, a function is continuous if, for every open set in the target space (\(Y\)), the preimage in \(X\) is also an open set. Otherwise, it is not continuous. In the first example, the function \(f\) is continuous because every time we take an open set in \(Y\), we obtain an open set in \(X\). The function \(g\) is not continuous because this is not true for all open sets.
Definition of a Homeomorphism
Given two topological spaces \( X \) and \( Y \), and a bijective function \( f: X \to Y \) with an inverse \( f^{-1}: Y \to X \), if both \( f \) and \( f^{-1} \) are continuous, then \( f \) is called a homeomorphism, and the spaces \( X \) and \( Y \) are said to be homeomorphic \( X \cong Y \).
Homeomorphic spaces are also known as topologically equivalent.
What does this mean?
Being homeomorphic or topologically equivalent means that the two spaces are "essentially the same" from a topological perspective, even if their geometric shapes might look different.
This definition highlights the key properties of a homeomorphism:
- Bijection: The function \( f: X \to Y \) must be one-to-one and onto, meaning that each element of \( X \) corresponds to exactly one element in \( Y \), and vice versa.
- Continuity of \( f \): The function \( f \) must be continuous, meaning that the preimage of any open set in \( Y \) is an open set in \( X \).
- Continuity of \( f^{-1} \): The inverse function \( f^{-1}: Y \to X \) must also be continuous, which means that the preimage of any open set in \( X \) under \( f \) is an open set in \( Y \).
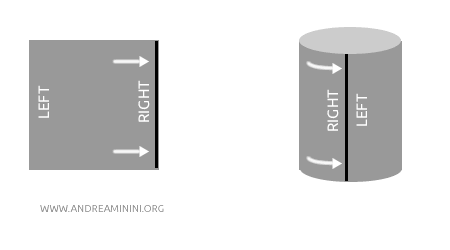
Example: Imagine taking a sheet of paper and rolling it into a cylinder. The cylinder and the flat sheet are homeomorphic because you can "transform" the cylinder into the flat sheet without tearing or gluing - just by unrolling it, and vice versa. The topology (the structure of open sets) remains the same, even though the geometric shape changes.
It’s important to note that the continuity of a bijection \( f \) does not automatically mean that its inverse \( f^{-1} \) is continuous, unless \( f \) is also an open map.
In other words, if the function \( f \) is continuous and bijective, this does not necessarily ensure that its inverse \( f^{-1} \) is continuous, and thus that the function is a homeomorphism.
In topology, a function \( f: X \rightarrow Y \) is considered continuous if the preimage of every open set in \( Y \) is an open set in \( X \).
However, this does not guarantee that the image of every open set in \( X \) under \( f \) will be open in \( Y \).
For the inverse function \( f^{-1} \) to be continuous, \( f \) needs to be not only continuous and bijective but also an open map.
Example
Consider the following two topological spaces:
- \( X = (a, b) \) with topology \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
- \( Y = (1, 2) \) with topology \( T_Y = \{\emptyset, Y\} \).
Define a function \( f: X \to Y \) such that \( f(a) = 1 \) and \( f(b) = 2 \).
The function \( f \) is clearly bijective, as every element in \( X \) corresponds uniquely to an element in \( Y \) and vice versa.
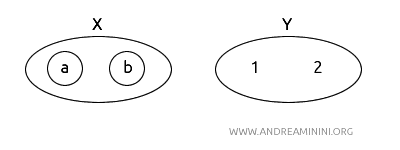
Note: In the diagram, open sets are represented by circles. For instance, besides the sets themselves, {a, b}, {a}, and {b} are open in \( X \), while the set {1, 2} is open in \( Y \). By definition, the empty sets are open in every topology. For simplicity, they are not shown.
Now, let's analyze the continuity of \( f \) and its inverse \( f^{-1} \).
- Continuity of the function \( f \)
To check if \( f \) is continuous, we need to verify that the preimage of each open set in \( Y \) through \( f \) is open in \( X \). The open sets of \( Y \) are \( \emptyset \) and \( Y \):- \( f^{-1}(\emptyset) = \emptyset \), which is open in \( T_X \)
- \( f^{-1}(Y) = X \), which is open in \( T_X \)
- Continuity of the inverse \( f^{-1} \)
Now, consider the inverse function \( f^{-1}: Y \to X \), defined as \( f^{-1}(1) = a \) and \( f^{-1}(2) = b \).
To verify the continuity of \( f^{-1} \), we need to check that the preimage of each open set in \( X \) through \( f^{-1} \) is open in \( Y \). The open sets of \( X \) are \( \emptyset \), \(\{a\}\), \(\{b\}\), and \( X \):- \( f^{-1}(\emptyset) = \emptyset \), which is open in \( T_Y \)
- \( f^{-1}(\{a\}) = \{1\} \), which is not open in \( T_Y \) because the only open set in \( T_Y \) containing \( 1 \) is \( Y \) itself
- \( f^{-1}(\{b\}) = \{2\} \), which is not open in \( T_Y \) for the same reason
- \( f^{-1}(X) = Y \), which is open in \( T_Y \)
In conclusion, \( f \) is bijective and continuous, but its inverse \( f^{-1} \) is not continuous. Therefore, \( f \) is not a homeomorphism.
This example illustrates that a bijective and continuous function does not necessarily mean that its inverse is also continuous.
Note: In this example, the lack of continuity of \( f^{-1} \) is related to the nature of open sets in \( X \) and \( Y \): \( X \) has "smaller" open sets (like \(\{a\}\) and \(\{b\}\)), while \( Y \) has a coarser topology, with only \( \emptyset \) and \( Y \) as open sets.
Example 2
Consider the following two topological spaces:
- \( X = (a, b) \) with topology \( T_X = \{\emptyset, \{a\}, X\} \).
- \( Y = (1, 2) \) with topology \( T_Y = \{\emptyset, \{1\}, Y\} \).
Define a function \( f: X \to Y \) such that \( f(a) = 1 \) and \( f(b) = 2 \).
Once again, the function \( f \) is bijective since every element in \( X \) has a unique correspondence with an element in \( Y \) and vice versa.
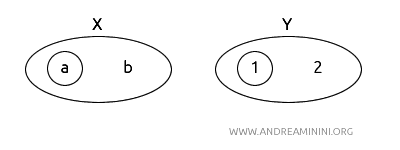
Let's examine the continuity of \( f \) and its inverse \( f^{-1} \).
- Continuity of the function \( f \)
To verify the continuity of \( f \), we need to check that the preimage of each open set in \( Y \) through \( f \) is open in \( X \). The open sets of \( Y \) are \( \emptyset \), \(\{1\}\), and \( Y \):- \( f^{-1}(\emptyset) = \emptyset \), which is open in \( T_X \)
- \( f^{-1}(Y) = X \), which is open in \( T_X \)
- \( f^{-1}(\{1\}) = \{a\} \), which is open in \( T_X \)
- Continuity of the inverse \( f^{-1} \)
Now, consider the inverse function \( f^{-1}: Y \to X \), defined as \( f^{-1}(1) = a \) and \( f^{-1}(2) = b \). To verify the continuity of \( f^{-1} \), we need to ensure that the preimage of each open set in \( X \) through \( f^{-1} \) is open in \( Y \). The open sets of \( X \) are \( \emptyset \), \(\{a\}\), and \( X \):- \( f^{-1}(\emptyset) = \emptyset \), which is open in \( T_Y \)
- \( f^{-1}(\{a\}) = \{1\} \), which is open in \( T_Y \)
- \( f^{-1}(X) = Y \), which is open in \( T_Y \)
In this case, \( f \) is bijective and continuous, and its inverse \( f^{-1} \) is also continuous. Thus, \( f \) is a homeomorphism.
The difference from the previous example lies in the choice of the topologies for the two spaces.
Note: This example demonstrates that with appropriate choices of topologies on \( X \) and \( Y \), it is possible to have a bijective and continuous function with a continuous inverse, unlike in the previous example where the continuity of the inverse was not guaranteed.
Distinguishing Homeomorphisms from Other Topological Transformations
While the term 'homeomorphisms' often broadly refers to topological transformations, they represent a specific subset of these transformations.
Topological transformations and homeomorphisms are closely related yet distinct:
- Topological transformations
This broader category includes any transformation that alters a topological space while preserving key topological properties like connectedness and continuity. Examples include not just homeomorphisms but also isotopies, homotopies, and diffeomorphisms. - Homeomorphisms
Specifically, a homeomorphism is a transformation that is both bijective and continuous, with a continuous inverse, allowing spaces to be transformed reversibly without alteration. Spaces that share a homeomorphic relationship are considered the same from a topological perspective, despite potential geometric differences.
While all homeomorphisms fall under the umbrella of topological transformations, not every transformation qualifies as a homeomorphism.
Some topological transformations may have unique features or limitations that do not align with the strict criteria of homeomorphisms.
Additional Notes
Here are some reflections and additional notes on homeomorphisms:
- Topological property
A topological property is a feature of a topological space that remains unchanged under a homeomorphism. In other words, if two topological spaces are homeomorphic (meaning there is a continuous, one-to-one mapping between them, with a continuous inverse), they share the same topological properties. - Hausdorff's Theorem on Homeomorphisms
The theorem states that if \( f: X \to Y \) is a homeomorphism and \( X \) is a Hausdorff space, then \( Y \) must also be a Hausdorff space. In other words, since homeomorphisms preserve topological properties, \( Y \) inherits the Hausdorff property from \( X \). - The equivalent concept of a homeomorphism in abstract algebra is a group isomorphism. In a group isomorphism, the bijective function maintains the algebraic structure of the group's operations. In contrast, a homeomorphism preserves the structure of open sets within topological spaces.
And so forth.
