Subspace Topology
Given a topological space \( (X, T) \), where \( X \) is a set and \( T \) is the collection of open sets defining the topology on \( X \), if \( Y \) is a subset of \( X \), the subspace topology on \( Y \) is defined by the collection: \[
T_Y = \{ U \cap Y \mid U \in T \}, \] where each open set in \( Y \) is the intersection of an open set in \( X \) with \( Y \). It is also called the induced topology.
In other words, a set \( V \subseteq Y \) is considered open in the subspace topology if it can be written as the intersection of \( Y \) with an open set \( U \) in the original space \( X \).
Thus, all open sets in the subspace topology $ Y $ are of the form \( U \cap Y \), where \( U \) is open in \( X \).
$$ V_{open \ in \ Y} = U \cap Y $$
Likewise, all closed sets in the subspace topology $ Y $ are of the form \( C \cap Y \), where \( C \) is closed in \( X \).
$$ V_{closed \ in \ Y} = C \cap Y $$
This means that a topological subspace is a subset of a topological space, equipped with a topology inherited from the original space.
Note. Open sets in the subspace topology $ Y $ might not be open in the topological space $ X $. In general, there can be sets that are open in Y but closed in X, or the other way around. Moreover, some sets might be open or closed in both Y and X. And of course, there can also be clopen sets, which are both open and closed. In the first example of these notes, I demonstrate such a case and explain why this occurs.
Practical Example
Consider the topological space \( \mathbb{R} \) with the standard topology, where the open sets are open intervals.
Let \( Y = [0, 1] \) be a subset of \( \mathbb{R} \).
The subspace topology on \( Y \) includes sets of the form:
$$ U \cap [0, 1] $$
where \( U \) is an open set in \( \mathbb{R} \).
For example, the set (-1, 0.5) is open in the topological space \( \mathbb{R} \).
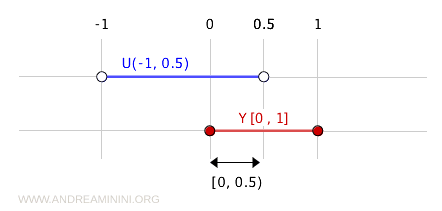
The intersection of (-1, 0.5) with the set \( Y = [0, 1] \) is an open set in the subspace topology on \( Y \).
$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$
Therefore, the set \( [0, 0.5) \) is open in the subspace \( Y \).
Conversely, the set $ [0, 0.5] $ is closed in the subspace topology on $ Y $ because it can be obtained by intersecting the closed set [-1, 0.5] in $ X $ with the set $ Y $.
$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$
In summary, the topological subspace \( Y \) inherits a topological structure from the original space \( X \) such that the open sets in \( Y \) are intersections of \( Y \) with the open sets of \( X \).
Note. Sets like [0,a) or (a,1], where 0<a<1, are closed in the standard topology on $ \mathbb{R} $ but are open in the subspace topology because they can be obtained as intersections between Y=[0,1] and an open set in $ \mathbb{R} $. For instance, consider the open set (-1,0.5) in $ \mathbb{R} $ and intersect it with Y=[0,1]: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ The interval [0,0.5) is open in the subspace Y even though it is not open in the standard topology on $ \mathbb{R} $.
Notice that there are sets that are open in both the subspace topology $ Y $ and in $ X $. For instance, the set (0.2, 0.8).
There are also sets that are closed in both the topology $ Y $ and in $ X $, such as the set [0.2, 0.8].
Finally, in the subspace topology \( Y = [0, 1] \), the set \( [0, 1] \) is both open and closed.
- Open
To prove that \( [0, 1] \) is open in the subspace \( Y \), we need to find an open set \( U \) in \( \mathbb{R} \) such that \( U \cap Y = [0, 1] \). We can simply choose \( U = \mathbb{R} \), which is obviously open in \( \mathbb{R} \). Then: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Therefore, \( [0, 1] \) is open in the subspace \( Y \). - Closed
To prove that \( [0, 1] \) is closed in the subspace \( Y \), we need to find a closed set \( C \) in \( \mathbb{R} \) such that \( C \cap Y = [0, 1] \). We can take \( C = [0, 1] \), which is closed in \( \mathbb{R} \). $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Thus, \( [0, 1] \) is closed in the subspace \( Y \).Note: Alternatively, we can demonstrate that \( [0, 1] \) is closed in \( Y \) by noting that the complement of \( [0, 1] \) in \( Y \) is the empty set, which is open in any topology. Since the complement of an open set is closed, it follows that \( [0, 1] \) is closed in \( Y \).
In conclusion, the set \( [0, 1] \) in the subspace topology \( Y = [0, 1] \) is both open and closed.
This type of set is also referred to as "clopen," a blend of the words "closed" and "open."
Example 2
Consider the standard topology on the set of real numbers \(\mathbb{R}\).
In this topology, any open set (a,b) with $ a > b $ is an open set.
A topological subspace of \(\mathbb{R}\) is the set of integers \(\mathbb{Z}\), because each integer can be obtained as the intersection of open intervals in the set of real numbers.
For instance, the integer 7 can be obtained by intersecting the open set (6.5,7.5) in \(\mathbb{R}\) with the set of integers \(\mathbb{Z}\).
$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$
In the same way, any other integer can be obtained.
Thus, each integer is an open set in the topological subspace of \(\mathbb{Z}\).
Similarly, any subset of \(\mathbb{Z}\) is also an open set in this subspace.
For example, to obtain the set {6,7,8}, you simply intersect the open set (5.5,8.5) with the set \(\mathbb{Z}\).
$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$
This topological subspace in \(\mathbb{Z}\) is also known as the discrete topology.
Note: The discrete topology on \(\mathbb{Z}\) is not a subspace of the standard topology on \(\mathbb{R}\); rather, it is a topology in its own right. However, the subspace topology that \(\mathbb{Z}\) inherits from the standard topology on \(\mathbb{R}\) is equivalent to the discrete topology on \(\mathbb{Z}\).
Example 3
Consider the three-dimensional Euclidean space \(\mathbb{R}^3\) with the standard topology where the open sets are unions of open balls.
Now, consider the unit sphere \( S^2 \), defined as the set of points in \(\mathbb{R}^3\) that are at a distance of 1 from the origin:
$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$
The subspace topology on \( S^2 \) is defined as follows:
$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ is open in } \mathbb{R}^3 \} $$
In other words, a set \( V \subseteq S^2 \) is open in the subspace topology if and only if it can be written as the intersection of \( S^2 \) with an open set \( U \) in \(\mathbb{R}^3\).
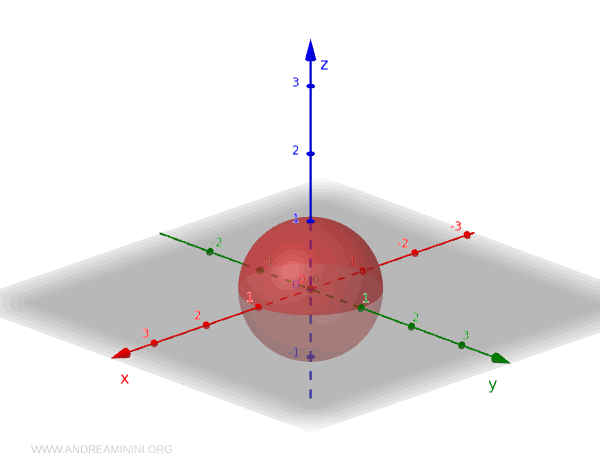
Here are some examples of open sets in \( S^2 \):
- Union of open subspaces in \(\mathbb{R}^3\)
Consider the open set \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \). The intersection of \( U \) with \( S^2 \) is: $$ U \cap S^2 = S^2 $$ because every point on \( S^2 \) satisfies \( x^2 + y^2 + z^2 = 1 \), which is clearly less than 2. Therefore, \( S^2 \) is open in itself. - A small portion of the sphere
Consider \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \text{ and } z > 0 \} \). This \( U \) represents the upper part of the unit sphere (upper hemisphere). The intersection with \( S^2 \) is: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ This set represents the upper part of the sphere and is open in the subspace topology \( T_{S^2} \). - Open sets and closure
The empty set \( \emptyset \) and \( S^2 \) itself are open in \( S^2 \).
- The finite intersection of open sets in \( S^2 \) is open in \( S^2 \).
- The arbitrary union of open sets in \( S^2 \) is open in \( S^2 \).
In summary, the sphere \( S^2 \) as a topological subspace of \(\mathbb{R}^3\) inherits its topological structure from the standard topology of \(\mathbb{R}^3\), where the open sets in \( S^2 \) are intersections of \( S^2 \) with open sets in \(\mathbb{R}^3\).
Properties of Subspace Topology
Here are the main properties of subspace topology:
- Open sets
The open sets in \( Y \) are all of the form \( U \cap Y \), where \( U \) is open in \( X \). - Empty and full sets
The empty set \( \emptyset \) and the set \( Y \) itself are always open in \( Y \):
- \( \emptyset \) is open because \( \emptyset = \emptyset \cap Y \).
- \( Y \) is open because \( Y = X \cap Y \). - Finite intersections
The intersection of a finite number of open sets in \( Y \) remains open in \( Y \). If \( V_1, \ldots, V_n \) are open in \( Y \), then: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ where each \( U_i \) is open in \( X \), and the finite intersection of open sets in \( X \) is open in \( X \). - Arbitrary unions
The arbitrary union of open sets in \( Y \) remains open in \( Y \). If \( V_\alpha \) is open in \( Y \) for each \( \alpha \) in some index set \( I \), then: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ where each \( U_\alpha \) is open in \( X \), and the arbitrary union of open sets in \( X \) is open in \( X \).
Notes
Some side notes on subspaces
- The standard topology on any subspace Y of \(\mathbb{R^n}\) is equivalent to the subspace topology of \(\mathbb{R^n}\).
Example. Consider the set Y=[-1,0)U(0,1], which is a subset of \( \mathbb{R} \). In the standard topology on Y, the intervals [-1,0) and (0,1] are both open because they can be obtained as intersections of Y with open sets in the standard topology on the real numbers \( \mathbb{R} \). For instance, consider the open sets (-1.5,0.5) and (0,1.5) in the standard topology on \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Therefore, the standard topology on Y is equivalent to the subspace topology of the standard topology on \( \mathbb{R} \). In this case, the intervals [-1,0) and (0,1] are also closed in the standard topology on Y because the complement of the open set [-1,0) is (0,1], making (0,1] a closed set. Similarly, the complement of the open set (0,1] is [-1,0) in the standard topology on Y, so [-1,0) is a closed set. In conclusion, the sets [-1,0) and (0,1] are both open and closed (clopen) in the standard topology on Y.
- Subspace Topology Basis Theorem
This theorem asserts that if we have a basis $ B_X $ for the topology of a topological space \(X\) and we consider a subset \(Y \subset X \), then the collection of sets formed by intersecting \( B \) with \(Y\) constitutes a basis $ B_Y $ for the subspace topology on \(Y\). $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$
And so forth.
