Basis Theorem in Subspace Topology

Given a topological space $X$ with a basis $ B_X $—a collection of open sets that "generates" the topology on $X$—and a subset $Y$ of $X$, the collection of intersections of the elements of $ B_X $ with $Y$ forms a basis $ B_Y $ for the subspace topology on $Y$. $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$

Example
Proof

Example

Let's make this concept clearer with a simple example.

Consider the topological space $ \mathbb{R} $ with the standard topology, which has as its basis the set of open intervals $(a, b)$, where $ a < b $.

Now, take the subset $Y = [0, 2]$ of $ \mathbb{R} $.

We want to find a basis for the subspace topology on $Y$.

The basis for the standard topology on the set of real numbers $ \mathbb{R} $ is:

$$ B_{\mathbb{R}} = \{(a, b) \ | \ a, b \in \mathbb{R}, \ a < b \} $$

Note: The basis for the real numbers is a collection of sets (a,b) with a<b where a and b are real numbers. Any open set in $\mathbb{R}$ can be expressed as a union of such open intervals. For example, the open set (0,3) can be obtained by uniting the open sets (0,2)U(1,3). Similarly, the open set (2,5) can be obtained by the union of the open sets (2,4)U(3,6).

The basis for the subspace topology on $Y$ is the intersection of all the open sets (a,b) in the basis of $ \mathbb{R} $ with the set $Y = [0,2]$ in the subspace topology.

$$ B_Y = \{ (a, b) \cap [0, 2] \ | \ (a, b) \in B_{\mathbb{R}} \} $$

Here are some elements that can be part of $ B_Y $:

For instance, take the open set $ (a, b) = (-1, 1) $ in the topology of $ \mathbb{R} $.

$$ (-1, 1) \cap [0, 2] = [0, 1) $$

So, $[0, 1) $ is an element that belongs to the basis $ B_Y $.

Next, take $ (a, b) = (1, 3) $ in the topology of $ \mathbb{R} $.

$$ (1, 3) \cap [0, 2] = (1, 2] $$

So, $ (1, 2] $ is another element of the basis $ B_Y $.

Now, take $ (a, b) = (0.5, 1.5) $ in the topology of $ \mathbb{R} $.

$$ (0.5, 1.5) \cap [0, 2] = (0.5, 1.5) $$

Thus, $ (0.5, 1.5) $ is also an element of $ B_Y $. And so on.

Let's verify the basis $ B_Y $:

Consider an open set $W$ in the subspace topology on $Y$, for example $W = (0.5, 1.5]$.

The set $W = (0.5, 1.5] $ is open in $Y$ because there exists an open set $U$ in $ \mathbb{R} $ such that $W = U \cap [0, 2]$. For example $U = (0.5, 1.5]$.

$$ W = U \cap [0, 2] = (0.5, 1.5] \cap [0, 2] = (0.5,1.5] $$

Consider a point $y \in W$, for example $ y = 1 $.

Since $U = (0.5, 1.5]$ is open in $ \mathbb{R} $, there exists a basis element $ (a, b) \in B_{\mathbb{R}} $ such that $ y \in (a, b) \subseteq U $.

In this case, we can take $ (a, b) = (0.8, 1.2) $.

Intersecting $ (a, b) $ with $ [0, 2] $ we get:

$$ (0.8, 1.2) \cap [0, 2] = (0.8, 1.2) $$

So, $ (0.8, 1.2) $ is an element of $ B_Y $ that contains $ y = 1 $ and is in $ W = (0.5, 1.5] $.

This confirms that every point of $ W $ is covered by an element of $ B_Y $, demonstrating that $ B_Y $ is a basis for the subspace topology on $Y$.

Proof

In topology, consider a subset $X \subset Y$.

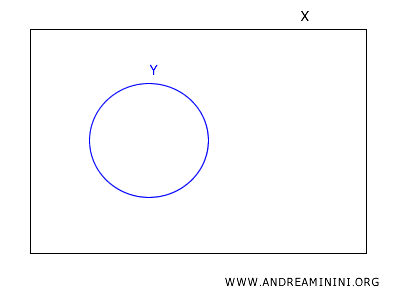
example

The basis $B_Y$ is the collection of sets formed by intersecting each element of the basis $B_X$ with the subset $Y$.

Each element of $B_Y$ is an open set in the subspace topology on $Y$.

We need to show that $B_Y$ is a basis for the subspace topology on $Y$.

Let's consider an open set $W$ in the subspace topology on $Y$.

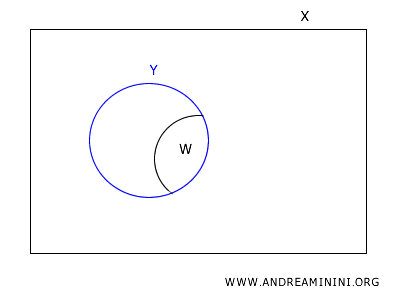
example

Since $W$ is open in $Y$, there exists an open set $U$ in $X$ such that $W = U \cap Y$.

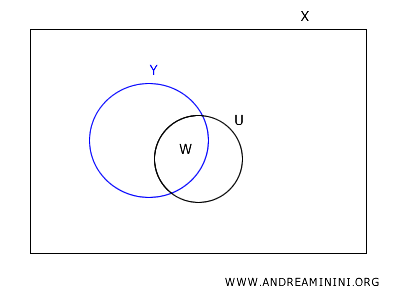
example

Take any point $y$ in $W$.

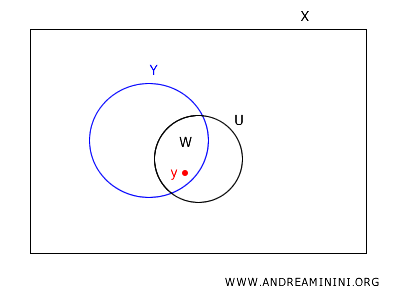
example

Since $U$ is open in $X$, by the definition of a basis, there exists a basis element $B \in B_X$ such that $y \in B \subseteq U$.

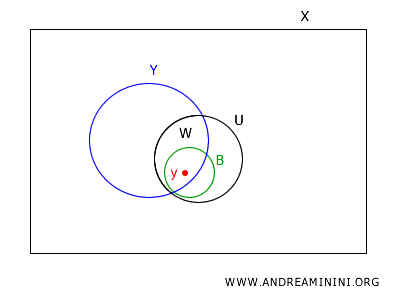
example

Intersecting $B$ with $Y$, we obtain $B \cap Y \in B_Y$, which contains $y$ and is contained within $W$. Hence, every point in $W$ is covered by an element of $B_Y$.

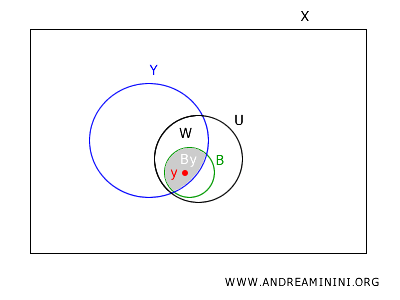
example

In conclusion, every point $y$ in $W$ is contained in an element of $B_Y$ which is also contained in $W$.

$$ y \in B_Y = B \cap Y \subseteq U \cap Y = W $$

This demonstrates that $B_Y$ is a basis for the subspace topology on $Y$.

And so on.