The Standard Topology of an Open Set

The standard topology on R defines every open interval (a, b) where a < b, and any finite or infinite union of such intervals, as an open set.

This stipulates that a set U is open if, for every point x in U, there is an open interval (a, b) such that x falls within (a, b) and (a, b) is a subset of U.

$$ x \in (a,b) \subseteq U $$

In essence, each element x of the open set U is contained within an interval (a, b) that is also part of U.

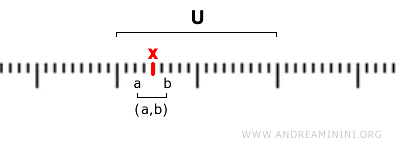
example of an open set

Therefore, the following are considered open sets in the standard topology:

Open Intervals
Open sets in the standard topology on $ \mathbb{R} $ are defined as open intervals $ (a, b) $, where a < b, and any union, no matter whether finite or infinite, of these open intervals $ (a, b) $.
Set Operations
Open sets also include unions and finite intersections of open sets.
- Unions: A union of any number of open sets, regardless of size, is always considered an open set.
- Finite Intersections: An intersection of a finite number of open sets also qualifies as an open set.

The standard topology is merely one among many possible topologies that can be defined on an open set X, but it is named "standard" due to its significance and widespread use across various mathematical disciplines.

This topology is chosen for its ability to effectively represent intuitive notions of proximity, openness, and continuity, especially on the real line R.

Note: Alternative topologies on R or other sets may have different bases, leading to open sets that follow different rules from the standard topology. Typically, these are designed to explore different properties or to examine mathematical scenarios in new ways.

Practical Example

The base of the standard topology on the real line R consists of all open intervals (a, b) with a < b.

$$ B = \{ (a,b) \subset; R \ | \ a<b \} $$

A critical aspect of this topology is that for any point x inside an interval, it is possible to find a smaller open interval around that point, entirely contained within the original interval, thereby meeting the definition of an open set in the standard topology.

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

Where U is an open set under the standard topology on R.

This topology is termed "standard" because it is the most commonly applied on the real line.

Example 2

Consider the real number interval (0,1), excluding both 0 and 1, and apply the standard topology.

I need to determine if it constitutes a topological space.

the case of the interval (0,1)

In practice, a subset $ U \subset (0, 1) $ is open in $ (0, 1) $ if for each point $ x \in U $, there is an open interval $ (a, b) $ in $ \mathbb{R} $ such that $ x \in (a, b) $ and $ (a, b) \cap (0, 1) \subseteq U $.

However, it suffices to note that the interval (0 ,1) is an intersection of open sets from R's standard topology.

Thus, the interval $ (0, 1) $ forms a topological space with the topology induced by the standard topology of $ \mathbb{R} $.

For instance, $ (0.1, 0.5) $, $ (0.2, 0.9) $, or their union, such as $ (0.1, 0.5) \cup (0.6, 0.8) $, all qualify as open sets in $ (0, 1) $ per the induced topology. In other words, the open sets within $ (0, 1) $ are those already included in R but restricted within $ (0, 1) $.

Since $ (0, 1) $ is a subspace of $ \mathbb{R} $ under the induced topology, it retains all fundamental properties of a topological space.

Example 3

Consider the finite set X={1,2,3}, consisting of three integers.

I need to assess whether it can be considered a topological space under the standard topology of $ \mathbb{R} $.

Here, the individual elements of X do not qualify as open sets because the standard topology of $ \mathbb{R} $ relies on open intervals as the basis for open sets, which does not directly apply to the set $ X $.

For example, if we treat the element {2} in the set X as a real number, it is contained within an open interval (2-ε, 2+ε) but the points of this interval are other real numbers not included in the set X. Thus, the definition of an open set under the standard topology in R is not met.
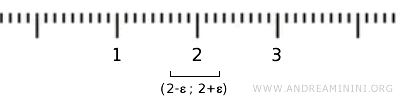
example with the number 2

While considering $ X $ as a subset of $ \mathbb{R} $, adopting the "induced topology" or "subspace topology" on $ X $ would limit the open sets to only the empty set and the set $ X $ itself, offering little topological interest.

For constructing a topological space with finite sets like $ X $, the discrete topology is preferable, where every subset of $ X $ is deemed an open set by definition.

And so forth