Convergence in a Topological Space

In a topological space $ X $, a point $ x \in X $ is called a limit point of the sequence $ (x_n) $ if, for every neighborhood $ U $ of $ x $, there exists a positive integer $ N $ such that for all $ n \geq N $, $ x_n \in U $.

In other words, the sequence $ (x_n) $ converges to $ x $ if, from some index $ N $ onward, all terms of the sequence lie within every neighborhood of $ x $.

Mathematically, this is expressed as:

$$ \lim_{n \to \infty} x_n = x $$

In this case, $ x $ is called the limit point of the sequence $ (x_n) $.

A Practical Example

Let's look at a concrete example with the sequence $ \frac{1}{x_n} $ in the topological space $ X = \mathbb{R} $ with the standard topology.

$$ x_n = \left( \frac{1}{n} \right) $$

I want to show that the sequence $ \left( \frac{1}{n} \right) $ converges to 0. That is, I want to prove that 0 is the limit point of the sequence $ \left( \frac{1}{n} \right) $.

To do this, I take any neighborhood $ U $ of 0.

In the standard topology of $ \mathbb{R} $, a neighborhood $ U $ of 0 contains an open interval of the form $ (-\epsilon, \epsilon) $ for some $ \epsilon > 0 $.

I need to find a positive integer $ N $ such that for every $ n \geq N $, $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Given $\epsilon > 0$, I can choose $ N = \left\lceil \frac{1}{\epsilon} \right\rceil $. Therefore, for every $ n \geq N $, we have:

$$ n \geq \frac{1}{\epsilon} \implies \frac{1}{n} \leq \epsilon. $$

Consequently, $ \left| \frac{1}{n} \right| < \epsilon $ for every $ n \geq N $.

Therefore, for every neighborhood $ U $ of 0, there exists an $ N $ such that for every $ n \geq N $, $ \frac{1}{n} \in U $. This proves that $ \lim_{n \to \infty} \frac{1}{n} = 0 $.

In summary, $ 0 $ is the limit point of the sequence $ \left( \frac{1}{n} \right) $.

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

Simply put, the sequence $ \frac{1}{n} $ converges to zero because, from a certain point onwards, all terms of the sequence fall within any neighborhood of zero.

Here is a table with the first ten values of the sequence:

$$
\begin{array}{|c|c|}
\hline
n & \frac{1}{n} \\
\hline
1 & 1 \\
2 & 0.5 \\
3 & 0.333 \\
4 & 0.25 \\
5 & 0.2 \\
6 & 0.167 \\
7 & 0.143 \\
8 & 0.125 \\
9 & 0.111 \\
10 & 0.1 \\
\hline
\end{array}
$$

For example, if I take $ N=5 $ where $ x_5= \frac{1}{5} = 0.2 $, for every $ n>5 $, the subsequent points belong to the same neighborhood $ U=(0 , 0.2) $.

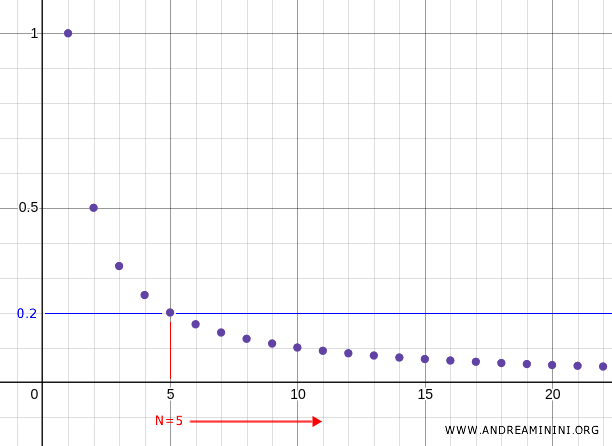
example of limit point

The same happens if I take any other value of $ N $.

For instance, if I consider $ N=10 $ where $ x_{10}=0.1 $, for every $ n>10 $, the sequence is contained within the neighborhood $ U = (0, 0.1) $, and so on.

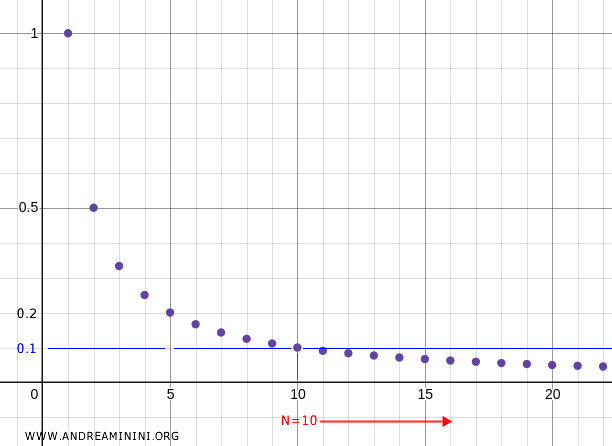
the sequence

Therefore, zero is the limit point of this sequence.

And so on.