Boundary of a Set

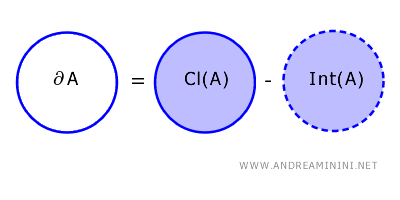
The boundary of a subset $A$ in a topological space $X$ is the set of points that belong to the closure of $A$ but not to its interior. $$\partial A = \text{Cl}(A) - \text{Int}(A)$$

Where $\text{Cl}(A)$ is the closure of $A$, which includes all the points in $A$ and its limit points.

Meanwhile, $\text{Int}(A)$ is the interior of $A$, consisting of all points in $A$ that have a neighborhood entirely contained within $A$.

It's essential to reiterate that the concept of a boundary is not an intrinsic property of a set; it depends on the topology employed.

Thus, the boundary of a set can vary when a different topology is utilized.

In other words, the boundary of a set $A$ consists of the points that are "close" to both the set $A$ and its complement $X \setminus A$.

A Practical Example

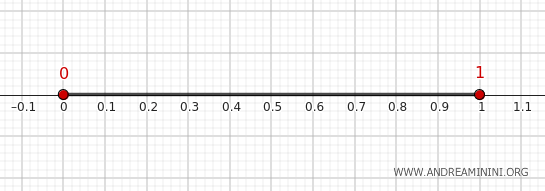
Consider the set $A = (0, 1)$ as a subset of the real line $\mathbb{R}$ in the standard topology.

Let's determine the boundary of $A$.

1] Calculate the Closure of A

The closure of $A$, denoted $\text{Cl}(A)$, includes all the points in $A$ and its limit points.

For $A = (0, 1)$, the closure is the closed interval $[0, 1]$ because every point in the interval $(0, 1)$ is a limit point, and the points 0 and 1 are the endpoints of the interval.

$$\text{Cl}(A) = [0, 1]$$

2] Calculate the Interior of A

The interior of $A$, denoted $\text{Int}(A)$, consists of all points in $A$ that have a neighborhood entirely contained within $A$.

For $A = (0, 1)$, the interior is the same set $(0, 1)$ because every point within the open interval has a neighborhood entirely within $(0, 1)$.

$$\text{Int}(A) = (0, 1)$$

3] Calculate the Boundary of A

The boundary of $A$, denoted $\partial A$, is defined as the set difference between the closure of $A$ and its interior:

$$\partial A = \text{Cl}(A) - \text{Int}(A)$$

Using the results from the previous steps:

$$\partial A = [0, 1] - (0, 1) = \{0, 1\}$$

Therefore, in the standard topology on $\mathbb{R}$, the boundary of the set $A = (0,1)$ is the set of points $\{0, 1\}$.

These two points are close to both the interior and exterior of $A$, thus representing the boundary of the set.

The Boundary Theorem

A point $x$ in a topological space $X$ belongs to the boundary $x \in \partial A$ of a subset $A$ if and only if every neighborhood of $x$ intersects both $A$ and $X - A$.

According to this theorem, to determine if a point $x$ belongs to the boundary of a set $A$, you check if every neighborhood of $x$ intersects both $A$ and $X - A$.

Example

Consider the set $A = (0, 1)$ on the real line $\mathbb{R}$ with the standard topology.

The closure and interior of this set are:

$$\text{Cl}(A) = [0, 1]$$

$$\text{Int}(A) = (0, 1)$$

Thus, the boundary of the set $A$ consists only of the points 0 and 1.

$$\partial A = \text{Cl}(A) - \text{Int}(A) = [0, 1] - (0, 1) = \{0, 1\}$$

Let's verify if the points 0 and 1 belong to the boundary using the previous theorem.

1] Check Point 0

Consider a neighborhood of zero, $(0-\epsilon, 0+\epsilon)$ with $\epsilon > 0$.

This neighborhood intersects $A$ because every neighborhood of 0 contains points in $(0, 1)$.

The neighborhood also intersects $X - A$, which is $(-\infty, 0] \cup [1, \infty)$, as it contains points less than 0.

Since every neighborhood of 0 intersects both $A$ and $X - A$, we conclude that $0 \in \partial A$.

 

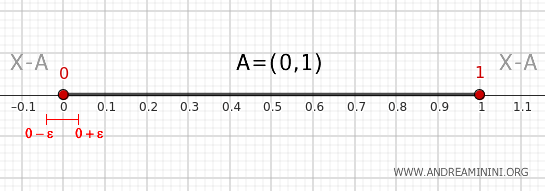
2] Check Point 1

Consider a neighborhood of 1, for instance, the interval $(1-\epsilon, 1+\epsilon)$ with $\epsilon > 0$.

This neighborhood intersects $A$ because every neighborhood of 1 contains points in $(0, 1)$.

The neighborhood also intersects $X - A$, which is $(-\infty, 0] \cup [1, \infty)$, as it contains points greater than 1.

Since every neighborhood of 1 intersects both $A$ and $X - A$, we conclude that $1 \in \partial A$.

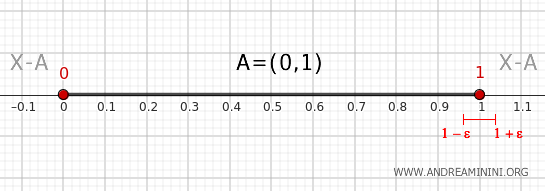
3] Check a Point Within (0,1)

Consider any point within the interval (0,1).

For example, the interval $(0.5-\epsilon, 0.5+\epsilon)$ with $\epsilon > 0$.

This neighborhood intersects $A$ because every neighborhood of 0.5 contains points in $(0, 1)$.

However, this neighborhood does not intersect $X - A$ because all points within this neighborhood belong to $A$.

Since there is a neighborhood of 0.5 that does not intersect $X - A$, we conclude that $0.5 \notin \partial A$.

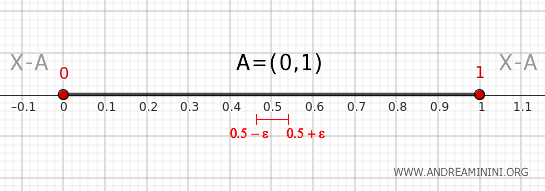
In conclusion, using the theorem, we verified that the points 0 and 1 belong to the boundary of $A = (0, 1)$, while an interior point like 0.5 does not. This confirms that the boundary of $A$ is $\{0, 1\}$.

Notes

Some observations and additional notes on set boundaries:

• Boundary $\partial A$ is a subset of $A$ if and only if $A$ is closed:
  $$\partial A \subseteq A \Leftrightarrow A \text{ è chiuso}$$
• Intersection of the boundary and the set A is empty if and only if A is open
  In other words, a set $A$ is open if and only if none of its points lie on its boundary.
  $$\partial A \cap A = \emptyset \Leftrightarrow A \text { is open}$$
• Boundary $\partial A$ is empty if and only if $A$ is both open and closed (clopen):
  $$\partial A = \emptyset \Leftrightarrow A \text{ is clopen}$$
• Boundary $\partial A$ coincides with the intersection of the closure of $A$ and the closure of $X-A$:
  $$\partial A = \text{Cl}(A) \cap \text{Cl}(X - A)$$
• Boundary $\partial A$ is always a closed set
  

  The intersection of two closed sets is always a closed set, which is a fundamental property in topological spaces. Since $\partial A$ is defined as the intersection of the two closed sets $\text{Cl}(A)$ and $\text{Cl}(X - A)$ $$\partial A = \text{Cl}(A) \cap \text{Cl}(X - A)$$ we can therefore conclude that $\partial A$ is always closed.

• Intersection of the boundary $\partial A$ and the interior $\text{Int}(A)$ is empty:
  $$\partial A \cap \text{Int}(A) = \emptyset$$
• Union of the boundary $\partial A$ and the interior $\text{Int}(A)$ is equal to the closure of $A$:
  $$\partial A \cup \text{Int}(A) = \text{Cl}(A)$$

And so on.