Boundary is a Subset of Set A if and Only if A is Closed

The boundary \( \partial A \) of the set \( A \) is a subset of \( A \) if and only if \( A \) is closed. \[ \partial A \subseteq A \Leftrightarrow A \text{ is closed} \]

Practical Example

Example 1

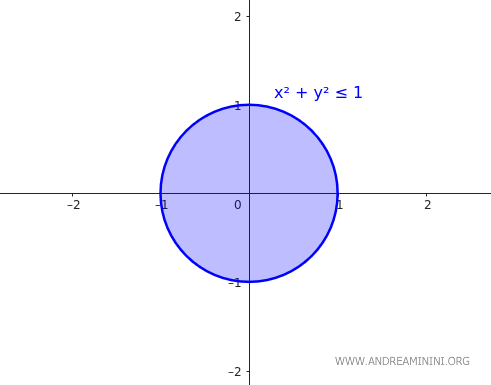
The set \( A \) is a closed circle with a radius of 1 centered at the origin in Euclidean space \(\mathbb{R}^2\).

$$ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 $$

The boundary of \( A \) in this case is the circumference of radius 1:

$$ \partial A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 $$

Since \( A \) is a closed circle, it contains all its boundary points. In particular, it includes all points on its boundary:

$$ \partial A \subseteq A $$

Therefore, \( A \) is closed.

Example 2

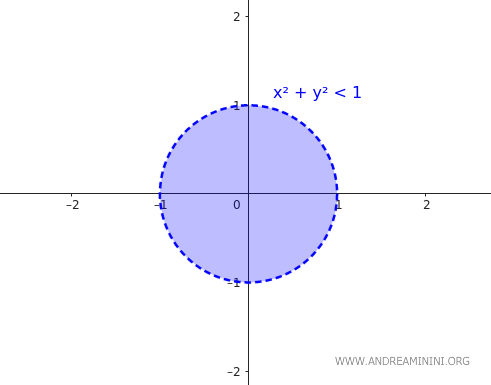
The set \( B \) is an open circle with a radius of 1 centered at the origin:

$$ B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 $$

The boundary of \( B \) is still the circumference of radius 1:

$$ \partial B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 $$

However, in this case, \( B \) does not include its boundary because \( B \) is defined as the open circle. Thus:

$$ \partial B \nsubseteq B $$

This shows that \( B \) is not closed.

These examples clearly illustrate how a closed set contains its own boundary, while an open set does not.

Proof

Let's divide the proof into two parts:

1] If the Boundary of A is a Subset of A, then A is Closed

Assume that \( \partial A \subseteq A \), meaning the boundary of \( A \) is a subset of \( A \).

We need to prove that the set \( A \) is closed.

The boundary of \( A \) is defined as \( \partial A = \overline{A} \cap \overline{A^c} \), where \( \overline{A} \) is the closure of \( A \) and \( \overline{A^c} \) is the closure of the complement of \( A \).

If the boundary of \( A \) is a subset \( \partial A \subseteq A \), then every point on \( \partial A \) is also in \( A \).

However, by definition of the boundary, every point on \( \partial A \) is also an accumulation point of \( A \) or \( A^c \).

To have \( \partial A \subseteq A \), \( A \) must contain all its accumulation points. This means \( A \) is closed, because by definition, a set is closed if it contains all its accumulation points.

2] If A is Closed, then its Boundary is a Subset of A

Assume the set \( A \) is closed. We need to prove that \( \partial A \subseteq A \), meaning its boundary is a subset of \( A \).

If \( A \) is closed, then it is equal to its closure $ \text{Cl}(A) $:

$$ A = \text{Cl}(A) $$

The boundary of \( A \) is the intersection between the closure of \( A \) and the closure of its complement \( A^c \):

$$ \partial A = \text{Cl}(A) \cap \text{Cl}(A^c) $$

Since \( \text{Cl}(A) = A \) because \( A \) is closed:

$$ \partial A = A \cap \text{Cl}(A^c) $$

The term \( A \cap \text{Cl}(A^c) \) represents points that are both in \( A \) and in the closure of the complement of \( A \).

However, if \( A \) is closed, the intersection \( A \cap \text{Cl}(A^c) \) contains only the points that belong to the boundary of \( A \).

Therefore, if \( A \) is closed, the boundary \( \partial A \) is contained in \( A \).

3] Conclusion

In conclusion, we have shown that \( \partial A \subseteq A \) if and only if \( A \) is closed.

And so on.