Hausdorff Space

A Hausdorff space is a type of topological space in which any two distinct points have separate open neighborhoods. This separation ensures that each point is uniquely isolated from every other point.

Simply put, in a Hausdorff space, you can always find open neighborhoods $ U $ and $ V $ for any two points $ x $ and $ y $ such that $ U $ and $ V $ do not overlap, i.e., $ U \cap V = \emptyset $.

This characteristic provides a measure of "separability" that mirrors our intuitive perception of distance and closeness as seen in Euclidean geometry.

Hausdorff spaces are prized in the fields of analysis and geometry because they allow for straightforward handling of sequences and their convergence.

A notable aspect of Hausdorff spaces is that single-point subsets are closed sets.

Therefore, the complement of any single point—which is the set comprising all other points—is always an open set.

Practical Examples
Remarks

Practical Examples

Example 1

Let's consider the standard topology, typically used to represent the real number line $\mathbb{R}$.

example of the real number line

In this topology, individual points are not open sets.

Explanation: An open set in this topology must include a complete open interval around each of its points. Since there are infinitely many numbers between any two real numbers, single points $ \{x\} $ fail to meet this requirement. They lack the surrounding space necessary to be included in an open set without encompassing adjacent points. Consequently, in the standard topology of the real number line, single points are not open.

However, the complement of each single point $ \mathbb{R} \setminus \{x\} $ is an open set.

the neighborhood of the single point is an open set

This implies that every single point $ \{x\} $ is a closed set since its complement is an open set.

The standard topology also qualifies as a Hausdorff space because it is always possible to find non-overlapping open intervals around any two distinct points $ a $ and $ b $ on $\mathbb{R}$.

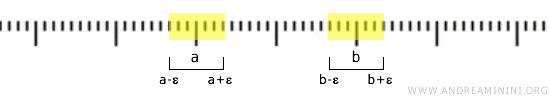
neighborhoods of points a and b

For instance, if $ a < b $, you can select the intervals $ (a-\epsilon, a+\epsilon) $ and $ (b-\epsilon, b+\epsilon) $ with $ \epsilon $ small enough that $ a+\epsilon < b-\epsilon $, ensuring the intervals remain disjoint.

Thus, the property of single points being closed in the standard topology corroborates the definition of a Hausdorff space.

Example 2

Let's consider a topological space composed of the set X = {1,2,3}, under the discrete topology.

In the discrete topology, every individual element (point) of X is considered an open set.

This implies that all possible subsets of $ X $ are open:

The empty set $ \emptyset $
The singleton sets $ \{1\} $, $ \{2\} $, $ \{3\} $
The two-element sets $ \{1, 2\} $, $ \{1, 3\} $, $ \{2, 3\} $, formed by unions or intersections of open sets
The entire set $ \{1, 2, 3\} $

In total, there are $ 2^3 = 8 $ open sets, corresponding to every subset of $ X $.

With discrete topology, this space is always a Hausdorff space.

By definition, a space is Hausdorff if for every pair of distinct points $ x $ and $ y $, there exist two open neighborhoods $ U $ and $ V $ such that $ U \cap V = \emptyset $ and $ x \in U $, $ y \in V $.

In this topology, selecting any two distinct points $ x $ and $ y $ from $ X = \{1, 2, 3\} $ allows for the simple choice of neighborhoods $ U = \{x\} $ and $ V = \{y\} $.

These neighborhoods are distinct ($ U \cap V = \emptyset $), fulfilling the Hausdorff condition.

For example, selecting x={1} and y={2} with neighborhoods U={1} and V={2}, results in their intersection being the empty set.

$$ \{ 1 \} \cap \{ 2 \} = \emptyset $$

This illustrates that the two elements have non-overlapping neighborhoods.

The same holds true when choosing any other pair of elements from X.

In the discrete topology, are individual points considered open or closed sets? When I first tackled this exercise, I was puzzled. If the discrete topology qualifies as a Hausdorff space, then individual points {x} ought to be closed. However, they are open by the very nature of the discrete topology. Why is this?

The solution is surprisingly straightforward, though initially counterintuitive: in topology, a set can be both open and closed, often referred to as clopen sets. In topology, "closed" isn't necessarily the opposite of "open".

In discrete topology, every single point {x} is also a closed set because its complement, which consists of all points other than x, is a union of open sets, thus itself an open set.

Therefore, if the complement of a single point {x} is open, it follows that the point {x} itself is also a closed set.

For instance, take the set X={1,2,3}; if you choose the element {1}, it is an open set by definition of discrete topology. However, it is also a closed set because its complement, X/{1}={2,3}, is open. The complement of an open set is invariably a closed set.

To summarize, individual points {x} in the discrete topology are both open and closed because each subset is open by definition, and the complements are open, making the points closed as well.

Open
In the discrete topology, every point is inherently an open set.
Closed
The complement, X/{x}, consisting of all other elements not in the subset {x}, is an open set. Since all points are open, their collective complements are open as well, thus making the point {x} a closed set.

In essence, the individual points {x} are open because every subset is open in the discrete topology, and they are closed because their complements are open.

A key distinction between the discrete and standard topologies is that in the standard topology, not all subsets are open. Only those subsets that fulfill the definition of an "open neighborhood" for each contained point are considered open.

Remarks

Some observations and notes on Hausdorff spaces

In a Hausdorff space, every convergent sequence of points converges to a unique point
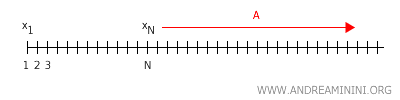
In a Hausdorff space X, every convergent sequence of points converges to a unique point x∈X. This is because if it converged to two or more distinct points, those points would have overlapping neighborhoods.
Proof. Let's consider a Hausdorff space X (e.g., the real line X=R). Suppose, for the sake of contradiction, that a convergent sequence of points x₁, x₂, x₃,... converges to two distinct points x and y in the space X. According to the definition of sequence convergence in a topological space, this means there is an integer N such that for every n>N, the points x_n are within the neighborhood A of x.

Conversely, there is also an integer M such that for every n>M, the points x_n are within the neighborhood B of y.

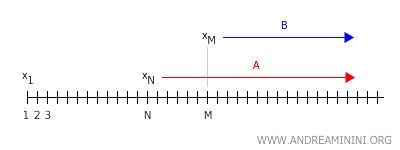
If M>N, then some of the points in neighborhood A of x would also belong to neighborhood B of y. The same would happen if N>M; in this case, some of the points in neighborhood B of y would also belong to neighborhood A of x. In either scenario, the intersection of the two neighborhoods of points x and y would not be empty $$ A \cap B \not = \emptyset $$ Therefore, the neighborhoods A and B are not disjoint. This contradicts a fundamental property of Hausdorff spaces, which states that for any pair of distinct points x and y in space X, there exist disjoint open neighborhoods ($ A \cap B = \emptyset $). Thus, in a Hausdorff space, a convergent sequence of points cannot converge to two or more distinct points. This assumption is false. Consequently, in a Hausdorff space, a convergent sequence can only converge to a unique point x in the space X.

And so forth.