Open Ball

In the realm of topology, an open ball—also referred to as a circular neighborhood, disk, or open sphere—is the collection of all points situated within a certain distance from a fixed point, known as the center (c). This distance is referred to as the radius (r). $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

This concept is set within a metric space (\( M \)), where \( d \) serves as a metric. A metric is essentially a function designed to measure the distance between any two points in space.

An open ball is distinctly characterized by its center and radius.

Described as "open" in a topological sense, this means that inside any given open ball, you can always find a smaller open ball that is completely contained within the larger one.

Note: Open balls are resilient to scaling and translations. In simpler terms, changing their size or moving them around doesn’t change their fundamental open ball nature.

Take, for example, the R² plane. Here, the Euclidean formula is used to pinpoint the distance between a point p=(x,y) and another chosen point c=(x₀,y₀) that serves as the center.

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

Open circular neighborhoods play a crucial role in defining the structure of topological spaces on planes and forming the foundation of a topology.

The standard topology of the R² plane is essentially a framework built upon an assortment of open balls.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

Here, p stands for a point p=(x,y) within the two-dimensional space, and r represents the radius of the circular neighborhood.

While this isn’t the sole topology for the plane, it's undeniably the most prevalent one.

In the context of an open ball, each point $ q \in B(p,r) $ is also at the heart of a smaller open ball B(q,ε), which itself is snugly fitted within B(p,r).

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ such \ that \ B(q,ε) \subset B(p,r) $$

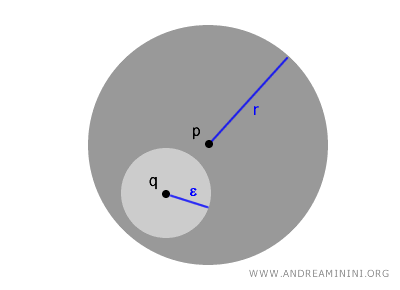
And the pattern continues.