Regular Spaces in Topology
A topological space \( X \) is called regular if it meets the following conditions:
- Single-point sets are closed, meaning every point in \( X \) is a closed set.
- Separation of points and closed sets: For any point \( a \in X \) and any closed set \( C \subset X \) that does not contain \( a \), there exist two disjoint open sets \( U \) and \( V \) such that: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
In topology, a regular space satisfies a stronger separation property than a Hausdorff space.
If a space is regular and has a countable base, then by Urysohn’s theorem, it is metrizable.
How does this compare to Hausdorff spaces?
Regular spaces ensure that a point and a disjoint closed set can be separated by distinct open sets. This is a stronger condition than in Hausdorff spaces, where only distinct points need to be separable by disjoint open sets.
Note. A regular space is not the same as a normal space. A normal space requires an even stronger condition: any two disjoint closed sets must be separable by disjoint open sets. This means that every normal space is automatically regular, but not every regular space is normal.
It’s worth noting that regularity is just one type of separation property, and a topological space can be regular without being Hausdorff, or vice versa. In fact, there are Hausdorff spaces that are not regular and regular spaces that are not Hausdorff.
A Practical Example
A classic example of a regular space is the real number line \( \mathbb{R} \) with the standard topology.
Consider a point \( x \in \mathbb{R} \) and a closed set \( C \) that does not contain \( x \).
For instance, let’s take \( x = 2 \) and the closed set \( C \):
\[ C = (-\infty, 0] \cup [5, \infty) \]
Clearly, \( x = 2 \notin C \), and \( C \) is closed in the standard topology.
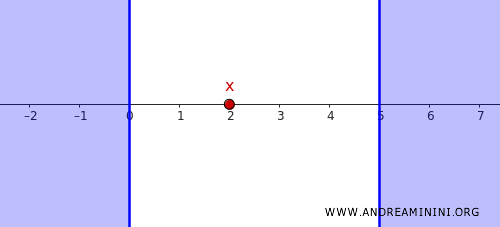
Now, we need to find open sets that separate \( x \) from \( C \).
The complement of \( C \) is an open set, so we can find an open interval that contains \( x \).
For example, the interval \( (0,5) \) contains \( x=2 \).
\[ (a, b) = (0, 5) \]
Now, we choose two values \( c \) and \( d \) that enclose \( x = 2 \):
\[ 0 < c < 2 < d < 5 \]
For instance, we take \( c = 1 \) and \( d = 3 \).
Next, we define two open sets:
- \( U = (c, d) = (1,3) \), which contains the point \( x = 2 \).
- \( V = (-\infty, c) \cup (d, \infty) = (-\infty, 1) \cup (3, \infty) \), which contains all of \( C \).
These two sets are disjoint, meaning \( U \cap V = \emptyset \), so they satisfy the regularity condition.
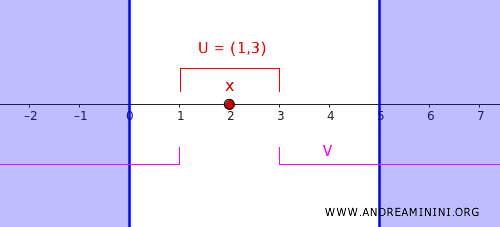
In conclusion, we have successfully separated the point \( x = 2 \) from the closed set \( C \) using two disjoint open sets, \( U \) and \( V \), demonstrating that the real number line with the standard topology is a regular space.
And so on.
