Normal Topological Space

A topological space $ X $ is said to be normal if it satisfies the following two conditions:

Singletons are closed sets
This means that for any point $ x \in X $, the set $\{x\}$ must be closed in the given topology.
Any two disjoint closed sets can be separated by disjoint open sets
If $ A $ and $ B $ are two closed sets that do not overlap (i.e., $ A \cap B = \emptyset $), then there exist two open sets $ U $ and $ V $ such that:
- $ A \subset U $
- $ B \subset V $
- $ U \cap V = \emptyset $ (they do not intersect).

The key idea behind normality is that in such spaces, you can always “enclose” two disjoint closed sets within separate open sets that do not touch each other.

In other words, normality ensures that whenever two closed sets are disjoint, we can always find disjoint open neighborhoods that contain them.

This property plays a fundamental role in constructing continuous functions that distinguish between points.

A Practical Example
Additional Notes

A Practical Example

Consider the topological space $ X = \mathbb{R} $ with the standard topology, which is generated by open intervals of the form $ (a, b) $.

Now, let’s take two disjoint closed sets in $ \mathbb{R} $ as an example:

$ A = \{0\} $, a single-point set.
$ B = [2, 3] $, a closed interval.

Both of these sets are closed in the standard topology of $ \mathbb{R} $, and since they have no points in common, they are also disjoint.

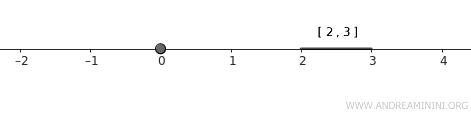
example

Note. The set $ A $ consists of a single point and does not include any of its surrounding area, making it closed. The set $ B $ is a closed interval, so it is also a closed set.

Now, we need to find two disjoint open sets that contain them.

One possible choice is $ U = (-1, 1) $, an open neighborhood that contains $ A = \{0\} $.

$$ A \subset U = (-1,1) $$

For $ B = [2,3] $, we can take $ V = (1, 4) $, an open neighborhood that fully contains it.

$$ B \subset V = (1,4) $$

These two open sets, $ U $ and $ V $, are disjoint since they do not overlap ($ U \cap V = \emptyset $).

This confirms that $ \mathbb{R} $ with the standard topology is a normal space.

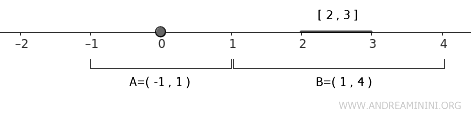
example

The same principle applies to any other pair of disjoint closed sets: we can always find disjoint open sets that contain them.

Thus, the real line $ X = \mathbb{R} $ with the standard topology is a normal space.

Additional Notes

Here are a few key points about normal spaces:

The real line $ \mathbb{R} $ with the standard topology is normal
Not only does it satisfy the regularity condition (meaning we can separate a point from a closed set using disjoint open sets), but it also meets the stronger requirement of normality.
Every metric space is normal
If a space has a metric that defines distances between points, then it is always normal.
Every normal space is also regular
This means normality is a stronger property than regularity.

And so on.