Boundary Theorem of a Set

A point $ x $ belongs to the boundary of a set $ A $ if every neighborhood of $ x $ intersects both the set $ A $ and the complement of $ A $ (i.e., $ X - A $).

In other words, if you can't find a neighborhood of $ x $ that lies entirely inside $ A $ or entirely outside $ A $, then $ x $ is on the boundary of $ A $.

A Practical Example
The Proof

A Practical Example

Let's look at a practical example to better understand this concept.

Consider the set $ A = (0, 1) $ on the real line $ \mathbb{R} $.

The points 0 and 1 are on the boundary of $ A $ because any neighborhood of 0 or 1 will always have a part inside $ (0, 1) $ and a part outside $ (0, 1) $.

Point 1
Any neighborhood $ (1-\epsilon, 1+\epsilon) $ with ε infinitesimally small has a part $ (1-\epsilon,1) $ within $ (0,1) $ and a part $ (1,1+\epsilon) $ outside $ (0,1) $. Thus, the point 1 is a boundary point of the set $ A $.
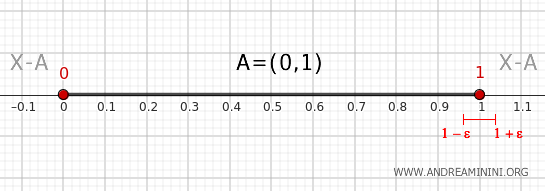
Point 0
Any neighborhood $ (0-\epsilon, 0+\epsilon) $ with ε infinitesimally small has a part $ (0,0+\epsilon) $ within $ (0,1) $ and a part $ (0-\epsilon,0) $ outside $ (0,1) $. Thus, the point 0 is also a boundary point of the set $ A $.
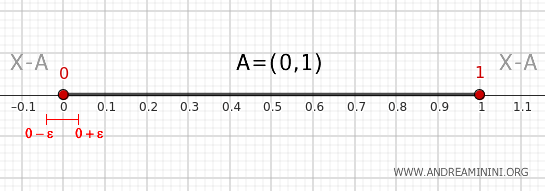
Point within the interval (0,1)
Any point $ x $ within the set has a neighborhood $ (x-\epsilon, x+\epsilon) $ with ε infinitesimally small that belongs to $ A = (0,1) $ but not to $ X-A $. Therefore, the interior points of the interval $ (0,1) $ are not boundary points.
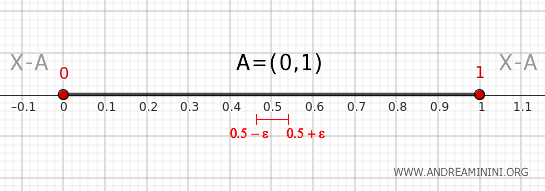
Point outside the interval (0,1)
Any point outside the interval $ (0,1) $, except for 0 and 1, has a neighborhood $ (x-\epsilon, x+\epsilon) $ with ε infinitesimally small that lies within $ X-A $ but not within $ A = (0,1) $. Hence, the points outside $ [0,1] $ are not boundary points of $ A $.

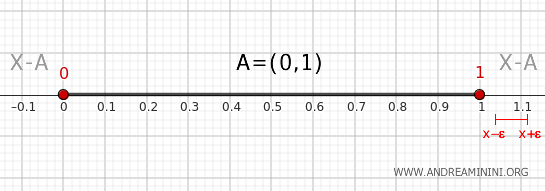
Therefore, the boundary points of the set $ A $ are the points 0 and 1.

$$ \partial A = \{0,1 \} $$

In summary, a point $ x $ is on the boundary of $ A $ if you can never find a neighborhood that lies entirely inside $ A $ or entirely outside $ A $. Is that clear now?

The Proof

To prove the theorem, I will consider two hypotheses:

1] The point $ x $ is a boundary point of $ A $

Consider a point $ x $ on the boundary of the set $ A $

$$ x \in \partial A $$

This implies that $ x \in \text{Cl}(A) $ and $ x \notin \text{Int}(A) $.

Since $ x \in \text{Cl}(A) $, every neighborhood of $ x $ intersects $ A $.

Moreover, since $ x \notin \text{Int}(A) $, every neighborhood of $ x $ is not a subset of $ A $ and thus must intersect $ X - A $.

Therefore, every neighborhood of $ x $ intersects both $ A $ and $ X - A $.

2] The point $ x $ intersects both $ A $ and $ X-A $

Now, suppose that every neighborhood of point $ x $ intersects both $ A $ and $ X - A $.

It follows that the point belongs to both sets $ x \in \text{Cl}(A) $ and $ x \in \text{Cl}(X - A) $.

Given that $ \text{Cl}(X - A) = X - \text{Int}(A) $, I deduce that $ x \notin \text{Int}(A) $.

Therefore, $ x \in \text{Cl}(A) $ and $ x \notin \text{Int}(A) $, meaning $ x \in \text{Cl}(A) - \text{Int}(A) = \partial A $.

This proves that the point $ x $ is a boundary point of $ A $.