Continuity of an inclusion function in topology

If $ X $ is a topological space and $ Y $ is a subset of $ X $, the inclusion function $ f : Y \to X $ is defined by $ f(y) = y $ for every $ y \in Y $. This function is continuous.

An inclusion function maps elements from a subset $ Y $ to its larger containing space $ X $.

In other words, the inclusion function $ f $ assigns each element of $ Y $ to the corresponding element in $ X $.

This function is continuous in a topological sense.

Note: The inclusion function is not the same as the identity function, although they may seem similar at first. The inclusion function maps from a subset to a larger space, while the identity function maps each element within a space to itself.

Why is it continuous?

In topology, a function is continuous if, for every open set $ U $ in $ X $, the preimage of $ U $ under $ f $, written as $ f^{-1}(U) $, is open in $ Y $.

According to the definition of the subspace topology, the open sets in $ Y $ are precisely the intersections of the open sets of $ X $ with $ Y $.

$$ f^{-1}(U) = U \cap Y $$

Since $ f^{-1}(U) = U \cap Y $ is always open in $ Y $ whenever $ U $ is open in $ X $, the function $ f $ is continuous by definition.

Note: This demonstrates how the subspace topology on $ Y $ is designed to ensure the inclusion function is continuous.

A practical example

Let’s consider the topological space $ X = \mathbb{R} $ (the real number line) and its subset $ Y = (0, 1) $, the open interval between 0 and 1.

The inclusion function $ f : Y \to X $ is defined by $ f(y) = y $ for all $ y \in Y $.

$$ f(y) = y \ \ \ \text{for all} \ \ y \in (0,1) $$

In simple terms, this means the function $ f $ "places" the points of $ Y $, which are the numbers in the open interval $ (0, 1) $, into the space $ X $, which is the entire real number line $ \mathbb{R} $.

In the subspace topology, for any open set $ U $ in $ X $, the intersection $ U \cap Y $ is an open set in $ Y $.

For example, take the open interval $ U = (-1, 0.5) \subset \mathbb{R} $ in the standard topology on $ X $.

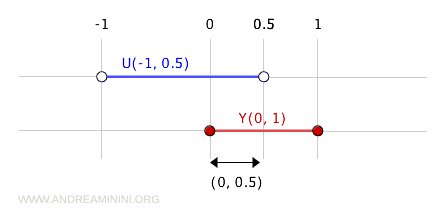
example

The intersection of this open set with $ Y = (0, 1) $ is:

$$ U \cap Y = (-1, 0.5) \cap (0, 1) = (0, 0.5) $$

This gives us an open interval within the set $ Y = (0, 1) $.

Thus, $ U \cap Y = (0, 0.5) $ is open in the subspace topology on $ Y $.

Since for every open set $ U $ in $ X $, the intersection $ U \cap Y $ is an open set in $ Y $, the inclusion function $ f : Y \to X $ is continuous.

And so on.