Subspace Theorem for Product Spaces

If we have two subsets $A$ and $B$ of topological spaces $X$ and $Y$ respectively, $$ A \subset X $$ $$ B \subset Y $$ the topology on the product $A \times B$, when considered as a subspace of $X \times Y$, is the same as the product topology on $A \times B$ constructed using the topologies on $A$ and $B$ inherited from $X$ and $Y$. $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$

Here, $\tau_{A \times B}^{\text{sub}}$ refers to the subspace topology on $A \times B$ induced by $X \times Y$,

while $\tau_A^{\text{sub}}$ and $\tau_B^{\text{sub}}$ are the subspace topologies on $A$ and $B$ inherited from $X$ and $Y$ respectively.

In essence, this theorem states that these two methods of defining the topology on $A \times B$ yield the same result.

The topology on $A \times B$ obtained as a subspace of $X \times Y$ is identical to the topology you would get by directly constructing the product topology on $A \times B$ using the inherited topologies of $A$ and $B$.

Thus, regardless of which approach you take, you will end up with the same topological structure on $A \times B$.

A Practical Example

Let’s illustrate this theorem with an example.

Consider two topological spaces $X$ and $Y$. For instance, think of the Cartesian plane, where $X$ is the $x$-axis and $Y$ is the $y$-axis.

Now, let’s look at two subsets of these spaces: $A$ as a subset of $X$, and $B$ as a subset of $Y$.

For example, $A$ might be an interval on the $x$-axis, say $[1, 2]$, and $B$ could be an interval on the $y$-axis, say $[3, 4]$.

The Cartesian product of these two subsets, $A \times B$, consists of all pairs $(x, y)$ where $x$ is taken from $A$ and $y$ is taken from $B$.

In this case, the Cartesian product forms a rectangle in the plane, with $x$ ranging from 1 to 2 and $y$ ranging from 3 to 4.

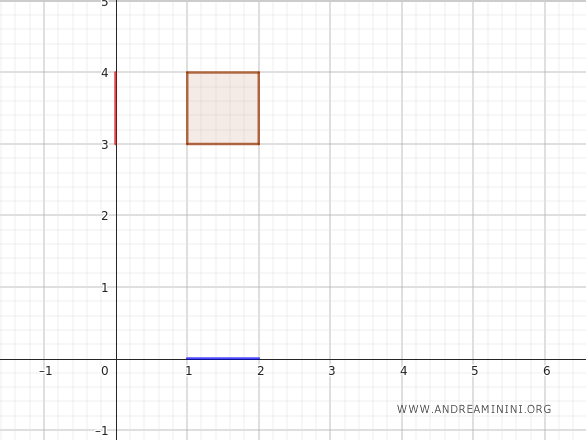
the subspace

Now, let’s consider two different topologies on $A \times B$:

Subspace Topology
Here, we consider $A \times B$ as a subspace of the product $X \times Y$, where $X \times Y$ represents the entire plane. This means we inherit the topology of $X \times Y$ and then restrict it to the subset $A \times B$.
Product Topology
Alternatively, we can directly construct a topology on $A \times B$ using the topologies of $A$ and $B$. In this approach, we treat $A$ as a topological space with the topology inherited from $X$, and $B$ as a topological space with the topology inherited from $Y$, then form the product topology on $A \times B$.

These two topologies, the subspace topology and the product topology, are actually the same.

So, no matter which method you choose, you will arrive at the same topological structure on $A \times B$.

And so on...