Intersection of Set Interiors

The intersection of the interiors of two sets $A$ and $B$ is equal to the interior of the intersection of those sets $ \text{Int}(A \cap B) $ $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$

In other words, the intersection of the interiors of two sets $A$ and $B$ is the same as the interior of their intersection.

To put it simply, if I take the points inside $A$ and the points inside $B$, and then find where these points overlap (i.e., take their intersection), I get exactly the points inside the set $A \cap B$.

There are two key concepts to understand:

Interior of a set ($\text{Int}(A)$): These are all the points in $A$ that are not on the "edge" of the set. Each interior point has a small circle around it that is completely contained within $A$.
Intersection ($\cap$): This is the set of all points that belong to both $A$ and $B$.

So, if I take the interior points of $A$ ($\text{Int}(A)$) and the interior points of $B$ ($\text{Int}(B)$), and then find the intersection of these two sets of points, I get exactly the interior of the set $A \cap B$.

A Practical Example
The Proof

A Practical Example

Imagine two circles $A$ and $B$ that partially overlap.

The interior of $A$ is the entire area of $A$ excluding its edge, and the same applies to $B$.

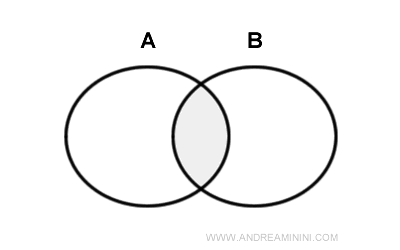
the intersection of sets

If I take the intersection of these two interior areas, I get exactly the interior area of the region where $A$ and $B$ overlap.

The Proof

The proof is in two steps:

1] First Inclusion ($\subseteq$)

If a point is inside set $A$ and also inside set $B$, then there is a small neighborhood around this point that is entirely within $A$ and also entirely within $B$.

Therefore, this neighborhood is also entirely within the intersection $A \cap B$, which means the point is in the interior of $A \cap B$.

Let $x \in \text{Int}(A) \cap \text{Int}(B)$. Then $x \in \text{Int}(A)$ and $x \in \text{Int}(B)$.

By definition of interior, there exist two open neighborhoods $U$ and $V$ such that $x \in U \subseteq A$ and $x \in V \subseteq B$.

Consider the neighborhood $W = U \cap V$. Since $U$ and $V$ are open, $W$ is also open and contains $x$.

Furthermore, $W \subseteq A \cap B$, since $W \subseteq U \subseteq A$ and $W \subseteq V \subseteq B$.

Thus, $x \in \text{Int}(A \cap B)$.

It follows that $\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)$.

2] Second Inclusion ($\supseteq$)

If a point is in the interior of $A \cap B$, then there is a small neighborhood around this point that is entirely within $A \cap B$.

Therefore, this neighborhood is also within set $A$ and within set $B$, which means the point is in the interior of both $A$ and $B$.

Let $x \in \text{Int}(A \cap B)$. Then there exists an open neighborhood $W$ of $x$ such that $W \subseteq A \cap B$.

Since $W \subseteq A \cap B$, we have $W \subseteq A$ and $W \subseteq B$.

Therefore, $x \in \text{Int}(A)$ and $x \in \text{Int}(B)$.

It follows that $x \in \text{Int}(A) \cap \text{Int}(B)$.

Thus, $\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)$.

Since I have demonstrated both inclusions, I can conclude that the two sets are equal:

\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]

The proof is complete.

And so forth.