Union of Interiors of Two Sets
The union of the interiors of two sets $ A $ and $ B $ is always included in the interior of the union of the two sets. \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] However, equality is not guaranteed.
This property highlights that the union of the interiors of two sets is always included in the interior of their union.
However, these two sets are not necessarily equal. In other words, it does not always hold that:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
It is possible for the inclusion to hold without equality.
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
This distinction helps to better understand the relationships between sets and their interiors in the context of topology.
A Practical Example
Consider two open intervals \( A \) and \( B \) in \(\mathbb{R}\) with the standard topology:
$$ A = (0, 2) $$
$$ B = (1, 3) $$
The interior of an open interval is the interval itself, so:
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
The union of the interiors is:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
The union of these two intervals is the interval that spans from the smallest point to the largest point, without repetition:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
The union of the intervals \( A \) and \( B \) is:
$$ A \cup B = (0, 2) \cup (1, 3) $$
Since the intervals overlap, the union can be simplified to:
$$ A \cup B = (0, 3) $$
The interior of the union \( A \cup B \) is:
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
Now we can verify the property:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
In this example, it is clear that the union of the interiors is contained within the interior of the union of the two sets.
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Additionally, in this specific case, equality also holds:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
In other cases, equality may not hold.
For example, if we consider these two closed intervals as sets $$ A = [0, 2] $$ $$ B = [2, 3] $$ The interiors of the two sets are $$ \text{Int}(A) = (0, 2) $$ $$ \text{Int}(B) = (2, 3) $$ The interior of the union $ A \cup B = [0, 3] $ is the set $ (0, 3) $ $$ \text{Int}(A \cup B) = (0,3) $$ Therefore, the inclusion holds because $ (0, 2) \cup (2, 3) $ is included in $ (0, 3) $ $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ However, equality does not hold because the point $ 2 $ is in the interior of the union $$ 2 \in \text{Int}(A \cup B) = (0, 3) $$ but it is not in the interior of Int(A) nor in the interior of Int(B): $$ 2 \not \in \text{Int}(A) $$ $$ 2 \not \in \text{Int}(B) $$ Therefore, point 2 is not in the union of the interiors: $$ 2 \not \in \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) $$ Thus, the two sets are not equal: $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ This shows that, in general, the union of the interiors of two sets is contained within the interior of the union, but equality does not always hold.
Example 2
Now consider two open intervals that do not overlap, for example:
$$ A = (0, 1) $$
$$ B = (2, 3) $$
The interior of each interval is the interval itself because they are both open:
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
The union of the interiors is:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
The union of the intervals \( A \) and \( B \) is:
$$ A \cup B = (0, 1) \cup (2, 3) $$
The interior of the union \( A \cup B \) is:
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
Now we can verify the property:
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
$$ \text{Int}(A \cup B) = \text{Int}((0, 1) \cup (2, 3)) = (0, 1) \cup (2, 3) $$
In this case as well, it is confirmed that:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
In these simple examples in \(\mathbb{R}\), I have demonstrated that the union of the interiors of two intervals is contained within the interior of the union of the two intervals, and in these specific cases, equality holds:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
However, as mentioned before, there are situations in more complex spaces where partial overlap can lead to containment without equality.
Example 3
Consider two sets \( A \) and \( B \) in the real plane \(\mathbb{R}^2\) with the standard topology.
The sets \( A \) and \( B \) are two open disks that partially overlap, centered at \( (0, 0) \) and \( (0.5, 0) \) respectively, both with radius \( 1 \):
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$
For open sets like \( A \) and \( B \), the interior of the set is the set itself. Therefore:
$$ \text{Int}(A) = A $$
$$ \text{Int}(B) = B $$
So, the union of the interiors is simply the union of the two disks:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
The union of the two sets \( A \) and \( B \) is a region composed of the two disks that partially overlap.
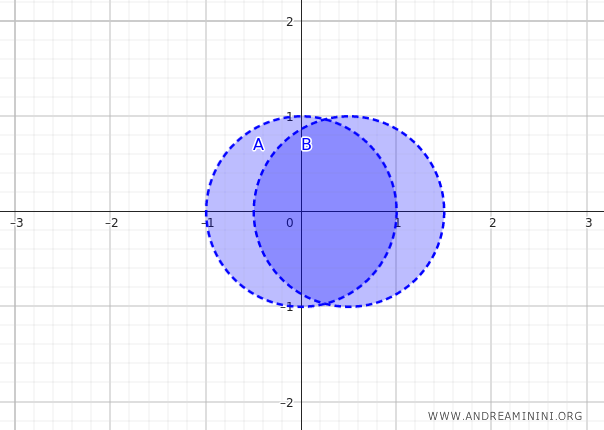
The interior of the union of the two sets \( A \) and \( B \) contains all points that have a neighborhood completely contained in \( A \cup B \).
$$ \text{Int}(A \cup B) = A \cup B $$
In this example too, the inclusion holds:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Proof
To prove the property of the union of the interiors, I need to show that the union of the interiors of two sets \( A \) and \( B \) is contained within the interior of the union of the two sets:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
I'll start the proof by recalling the definition of the interior of a set.
The interior of a set \( X \), denoted as \(\text{Int}(X)\), is the set of all interior points of \( X \).
Thus, a point \( x \) is an interior point of \( X \) if there exists a neighborhood of \( x \) completely contained in \( X \).
If I take a point \( x \in \text{Int}(A) \cup \text{Int}(B) \), this means that \( x \) must necessarily belong to \(\text{Int}(A)\) or \(\text{Int}(B)\).
- If \( x \in \text{Int}(A) \), then there exists a neighborhood \( U_x \) of \( x \) such that \( U_x \subseteq A \).
- If \( x \in \text{Int}(B) \), then there exists a neighborhood \( V_x \) of \( x \) such that \( V_x \subseteq B \).
In either case, whether \( x \in \text{Int}(A) \) or \( x \in \text{Int}(B) \), the neighborhood \( U_x \) or \( V_x \) of \( x \) is also contained in \( A \cup B \).
This implies that \( x \) is an interior point of \( A \cup B \).
Therefore, every point of \(\text{Int}(A) \cup \text{Int}(B)\) is also an interior point of \( A \cup B \). Consequently,
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
And that completes the proof.
