Power Set (Set of All Subsets)
What is the Set of All Subsets?
The Power Set or set of all subsets P(A) is the set containing all proper and improper subsets of A. $$ P(A) = \{ S | S \subseteq A \} $$ It's also known as the power set.
Each subset S={s1,...} is a part or component of the set A.
$$ S \subseteq A $$
Every subset S is also an element of the set of all subsets P(A).
$$ S \in P(A) $$
Note. In this case, the subset is an element because it belongs to the set P(A). That's why we use the membership relation S∈P(A). Here, S is not included in set P(A); S is only included in set A, meaning S⊆A.
A Practical Example of the Set of All Subsets
The set A consists of elements a and b.
$$ A = \{ a,b \} $$
The elements a,b are part of set A
$$ a,b \in A $$
Here's the Venn diagram of the set.
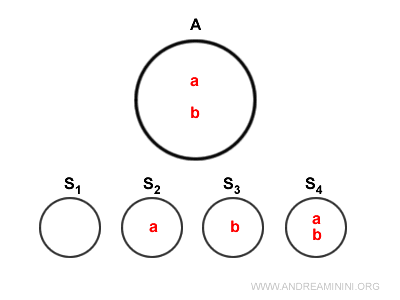
All subsets of A are part of the set of all subsets P(S).
$$ \{ \} \\ \{ a \} \\ \{ b \} \\ \{ a,b \} $$
Therefore, the set of all subsets is composed of the following elements:
$$ P(A) = \{ \{ \} , \{ a \} , \{ b \} , \{ a,b \} \} $$
that is
$$ P(A) = \{ ∅ , \{ a \} , \{ b \} , A \} $$
The subsets {a} and {b} are the proper subsets of A.
The subsets ∅ and A are the improper subsets of A.
Note. Being elements of P(A), I can also write $$ ∅ , \{ a \} , \{ b \} , A \in P(A) $$
Here's the Venn diagram of the set of all subsets P(A).
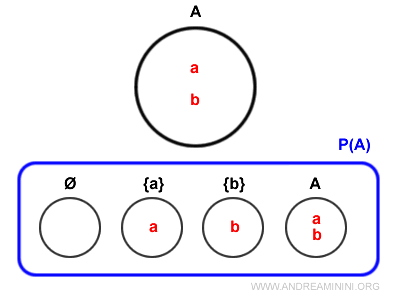
As you can see, even the set A is an element of the set of all subsets P(A) because every set is an improper subset of itself.
Why is there also the empty set?
In set theory, the empty set ∅ is a subset of any set.
Therefore, the empty set ∅ is also a subset of A.
For this reason, ∅ is an element of the set of all subsets P(A).
The Set of All Subsets of the Empty Set
In the case of an empty set A=∅, the set of all subsets is as follows:
$$ P(A) = \{ ∅ \} $$
I should clarify that {∅} is not the empty set but an element of the set of all subsets.
Why is the Set of All Subsets also called the Power Set?
The set of all subsets is also called the power set due to a specific property.
If a set A consists of n elements, the set of all subsets P(A) contains 2n elements.
Example
The set A={a,b} has n=2 elements.
The set of all subsets P(A) consists of 2n=22=4 elements.
Number of Subsets in a Set with n Elements
A set \( A \) with \( n \) elements has \( 2^n \) possible subsets.
To construct any given subset \( X \) of a set \( A \) with \( n \) elements, we must evaluate each element of \( A \) and decide whether to include it in \( X \) or not.
Since each element has exactly two choices—either being included or excluded—the total number of possible subsets is determined by multiplying these choices for all \( n \) elements. This leads to the formula:
\[ 2 \cdot 2 \cdot ... \cdot 2 = 2^n \]
Here, the factor \( 2 \) is multiplied by itself \( n \) times, once for each element in \( A \).
Note: This formula accounts for all possible subsets, including the empty set (which contains no elements) and the set itself (which contains all elements of \( A \)).
Example 1
Consider a set with \( n = 3 \) elements:
\[ A = \{a, b, c\} \]
Applying the formula to determine the total number of subsets:
\[ 2^3 = 8 \]
This means there are eight subsets:
\[ \emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \]
Among these, we find both the empty set \( \emptyset \) and the entire set \( A \).
Example 2
Now, let's take a set with \( n = 4 \) elements:
\[ B = \{1, 2, 3, 4\} \]
The number of subsets is:
\[ 2^4 = 16 \]
Once again, these subsets include the empty set, individual elements, pairs, triplets, and the entire set.
Thus, the number of subsets of a finite set always follows the same rule: for a set with \( n \) elements, the total number of subsets is given by \( 2^n \).
And so on.
