Partially Ordered Set

A set equipped with a partial order is called a partially ordered set, or poset for short. It is denoted by (A, ≤).

What is a partial order?

Given a set A, a partial order is a relation

$$ ≤:A \times A \rightarrow \{ \text{true}, \text{false} \}. $$

In other words, for any pair (x, y) in A, we can determine whether the order relation ≤ holds or not.

A concrete example

Consider a finite set A with 7 elements:

$$ A = \{ a, b, c, d, e, f \} $$

We define a relation ≤ on the Cartesian product A × A:

$$ ≤ = \{ (a,c), (a,e), (b,d), (b,f), (c,g), (d,g), (e,g), (f,g) \} $$

The pair (A, ≤) defines a poset.

Note. The relation is not defined for every pair of elements in the set - for example, there is no relation between (a, b), (a, d), and so on.

The relations in the poset (A, ≤) can be represented graphically as follows:

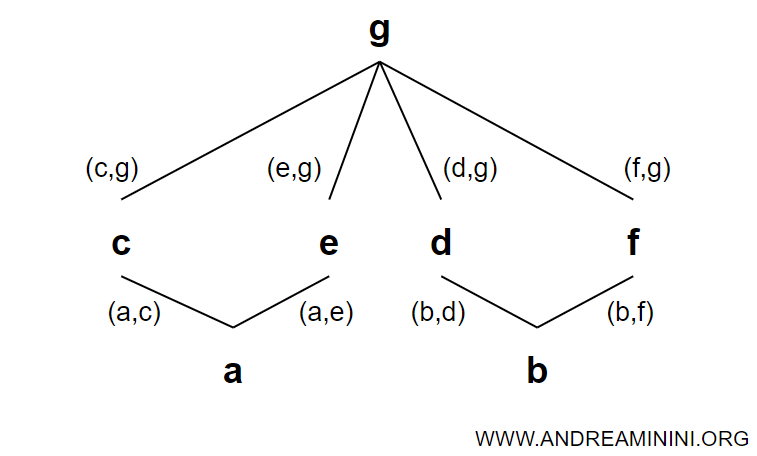
Each relation is shown as an arrow connecting the elements it relates.

Further examples of posets

• The natural numbers
  The set of natural numbers \( (\mathbb{N}, \leq) \) forms a poset under the standard “less than or equal to” relation, which is reflexive, antisymmetric, and transitive.

  For instance, if we take any two natural numbers from \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \), we can always determine whether one is less than or equal to the other.

• The power set ordered by inclusion
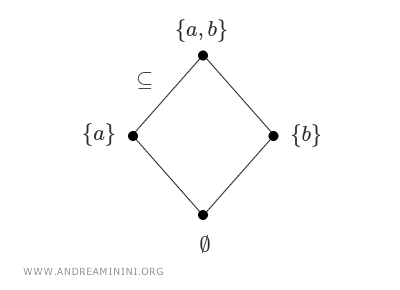
  Given a set \( S \), its power set \( \mathcal{P}(S) \) - the set of all subsets of S - forms a poset under the subset relation (\(\subseteq\)). In this case, the ordering is based on set inclusion rather than numeric comparison.
  

  For example, if \( S = \{a, b\} \), then \( \mathcal{P}(S) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} \). Here, the empty set Ø is a subset of every other set, and both {a} and {b} are subsets of {a, b}, whereas {a, b} is not a subset of either {a} or {b}. $$ \emptyset \subseteq \{ a \} \\ \{ a \} \subseteq \{a, b\} \\ \{ b \} \subseteq \{a, b\} \\ \vdots $$ These inclusion relations can be visualized using a lattice diagram, where each node represents a subset and each edge denotes inclusion from bottom to top.
  

• Divisibility among integers
  Another example of a poset is the set of integers \( \mathbb{Z} \) ordered by divisibility. The relation \( x \mid y \) means that x divides y, and defines a partial order on subsets of integers.
  

  For example, 4 divides 8 (4 | 8), so the relation holds, but 6 does not divide 8, so 6 | 8 is false. Let’s consider the set S = {2, 4, 6, 8, 12, 24} with the divisibility relation. The Hasse diagram below shows each number as a node, and edges (or chains of edges) connect each divisor to its multiples, going from bottom to top.
  
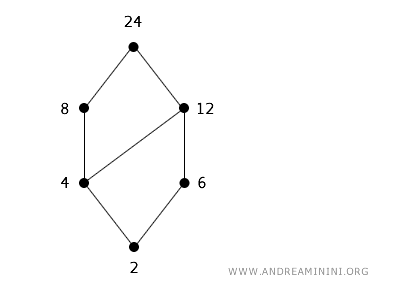
  Here, 2 divides all the others: 4, 6, 8, 12, and 24. However, the converse does not hold - for instance, 6 divides 12 and 24, but not 2, 4, or 8.

Key properties of a poset

A poset is a pair (S, ≤) consisting of a set S and a binary relation ≤ that satisfies the following properties:

• Reflexivity: Every element is related to itself: $$ \forall x \in S,\ x \le x $$
• Antisymmetry: If two elements relate to each other in both directions, they must be equal: $$ \forall x, y \in S,\ (x \le y \land y \le x) \Rightarrow x = y $$
• Transitivity: If x is less than y and y is less than z, then x is less than z: $$ \forall x, y, z \in S,\ (x \le y \land y \le z) \Rightarrow x \le z $$

In summary, a poset is a set equipped with a reflexive, antisymmetric, and transitive relation - but not necessarily a total one. This means that not all elements in the set must be comparable.

Posets are foundational in lattice theory and have applications in fields such as commutative algebra (e.g., the set of ideals of a ring) and algebraic topology.

Infimum and Supremum

Given a poset (A, ≤) and a subset B of A:

• The infimum of B, denoted inf(B), is the greatest element of A that is less than or equal to every element of B.
• The supremum of B, denoted sup(B), is the least element of A that is greater than or equal to every element of B.

Example

The subset B has both an infimum (3) and a supremum (4).

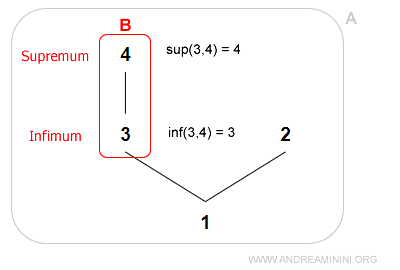
Note. A subset may not always have an infimum or supremum, but if they do exist, they are unique.

Lower and upper bounds

Given a poset (A, ≤) and a subset B of A:

• An element k in A is a lower bound of B if \( k \le b \) for every element \( b \in B \).

  Example. If A = {1, 2, 3, 4, 5, 6} and B = {3, 4}, then the lower bounds of B are {1, 2, 3}.

• An element k in A is an upper bound of B if \( k \ge b \) for every \( b \in B \).

  Example. With the same sets A and B, the upper bounds of B are {4, 5, 6}.

Maximal and minimal elements

In a poset (A, ≤):

• A minimal element is one that is not preceded by any other element in A.

  Example. In A = {1, 2, 3, 4, 5, 6}, the minimal element is 1.

• A maximal element is one that is not followed by any other element in A.

  Example. In the same set, the maximal element is 6.

A poset can have more than one maximal or minimal element.

Example

This diagram shows three maximal elements and one minimal element.

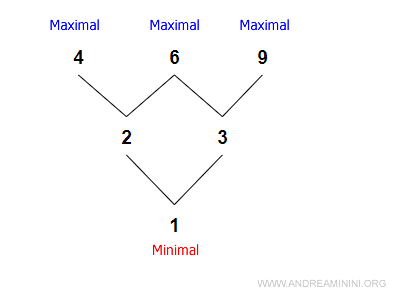
The ordering relation is defined as:

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

From this, we see that:

• 4, 6, and 9 are not followed by any other elements - they are maximal.
• 1 is not preceded by any element - it is minimal.

Note. Infinite posets may not have maximal or minimal elements. Finite posets, however, always have at least one of each.

Maximum and minimum

In a poset (A, ≤):

• The minimum is the unique element that is less than or equal to every other element in A.
• The maximum is the unique element that is greater than or equal to every other element in A.

Not every poset has a minimum or a maximum.

Example

Here, 1 is the minimum, but there is no maximum.

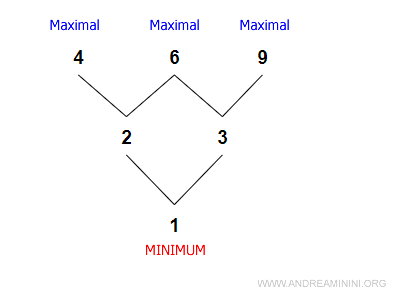
The ordering relation is:

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

We can verify that 1 is the minimum, since:

$$ 1 \leq 2 \\ 1 \leq 3 \\ 1 \leq 4 \\ 1 \leq 6 \\ 1 \leq 9 $$

However, we cannot conclude that 9 is the maximum because we lack information about (2,9), (4,9), and (6,9):

$$ 1 \leq 9 \\ 3 \leq 9 \\ 2 \; ? \; 9 \\ 4 \; ? \; 9 \\ 6 \; ? \; 9 $$

Likewise, for the other maximal elements:

4 is not the maximum since we don’t know whether (4,9), (4,6), or (4,3) hold:

$$ 1 \leq 4 \\ 2 \leq 4 \\ 4 \; ? \; 3 \\ 4 \; ? \; 6 \\ 4 \; ? \; 9 $$

6 is not the maximum either, because we don't know the status of (6,4) and (6,9):

$$ 1 \leq 6 \\ 2 \leq 6 \\ 3 \leq 6 \\ 4 \; ? \; 6 \\ 9 \; ? \; 6 $$

And so on.