Lattices

A lattice is a partially ordered set A in which every pair of elements (x, y) defines a subset B that has both a greatest lower bound and a least upper bound.

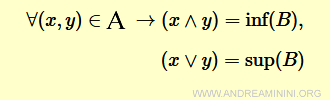
Specifically:

• The greatest lower bound is the largest element that is less than or equal to both x and y.

  This operation is known as the meet, or intersection, and is denoted by $$ x ∧ y \:\: = \:\: inf(x,y) $$

• The least upper bound is the smallest element that is greater than or equal to both x and y.

  This is called the join, or union, and is denoted by $$ x ∨ y \:\: = \:\: sup(x,y) $$

An Example of a Lattice

The figure below shows two partially ordered sets (A,≥).

One of them forms a lattice, the other does not.

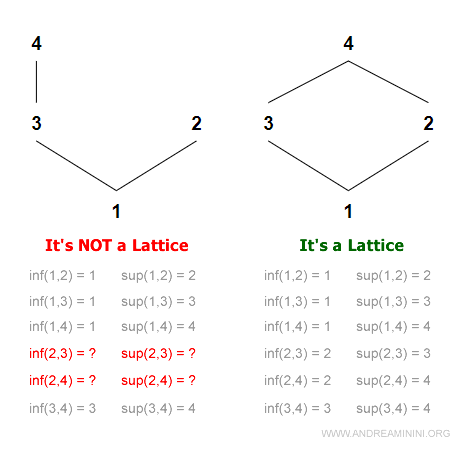
In the first poset, the pairs (2,3) and (2,4) lack both meet and join - i.e., there is no common lower or upper bound that satisfies the lattice condition.

In contrast, every pair of elements in the second set - considered as part of the Cartesian product - has both a meet and a join.

This makes the second set a proper lattice.

Further Examples of Lattices

 

The Algebraic Lattice

An algebraic lattice (L, ∧, ∨) is a lattice equipped with two binary operations: meet (∧) and join (∨), which are interpreted as multiplication and addition, respectively.

In any lattice, the following operations are defined:

• ∧ - called "and" (also known as conjunction)
• ∨ - called "or" (also known as disjunction)

These operations must satisfy the following axioms for all elements x and y in the partially ordered set:

• Commutativity

  $$ x ∧ y = y ∧ x $$ $$ x ∨ y = y ∨ x $$

• Associativity

  $$ x ∧ (y ∧ z) = (x ∧ y) ∧ z $$ $$ x ∨ (y ∨ z) = (x ∨ y) ∨ z $$

• Absorption

  $$ x ∧ (x ∨ y) = x $$ $$ x ∨ (x ∧ y) = x $$

• Idempotency

  $$ x ∧ x = x $$ $$ x ∨ x = x $$

Note: The first two properties - commutativity and associativity - are foundational in many branches of mathematics. The latter two - absorption and idempotency - are specific to lattices. It’s also worth noting that lattices, in general, do not require the distributive property.

Example

Consider a set consisting of just two subsets, a and b:

$$ L = \{ a , b \} $$

Graphically, the structure appears as follows:

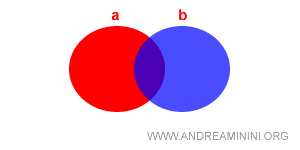
The operations are defined as:

• ∧ = ⋂ (intersection)
• ∨ = ∪ (union)

We want to determine whether the set (L, ⊆) qualifies as a lattice.

This involves checking whether the four lattice laws are upheld:

Commutativity

For two elements a and b:

$$ a \cup b = b \cup a $$

$$ a \cap b = b \cap a $$

Both conditions are satisfied.

Associativity

For three elements a, b, and c:

$$ a \cup (b \cup c) = (a \cup b) \cup c $$

$$ a \cap (b \cap c) = (a \cap b) \cap c $$

These also hold.

Absorption

For any two elements:

$$ a \cup (a \cap b) = a $$

$$ a \cap (a \cup b) = a $$

Both identities are satisfied.

Idempotency

For any element:

$$ a \cup a = a $$

$$ a \cap a = a $$

Again, both properties are met.

Since all four properties are fulfilled, we conclude that the set of subsets forms a valid lattice.

How to Tell If a Partially Ordered Set Is a Lattice

To determine whether a partially ordered set is a lattice, we need to verify whether the structure (A, r) satisfies the defining properties of lattices.

Example 1

Consider the set A with a divisibility relation denoted by the symbol |:

$$ ( A = \{1,2,3,4,5,6,7,12 \}, \ | ) $$

We define two operations based on divisibility:

• ∧ = GCD (Greatest Common Divisor)
• ∨ = LCM (Least Common Multiple)

We want to determine whether the partially ordered set (A, |) forms a lattice. This requires that for every pair of elements (a, b), both the greatest lower bound (infimum) and the least upper bound (supremum) exist within A:

$$ \forall (a, b) \in A^2, \ \inf(a,b) \in A $$

$$ \forall (a, b) \in A^2, \ \sup(a,b) \in A $$

Let’s examine the pair (4, 6):

$$ 4 ∧ 6 = \text{GCD}(4,6) = 2 \in A $$

$$ 4 ∨ 6 = \text{LCM}(4,6) = 12 \in A $$

Both the meet and the join are elements of A.

Now take a different pair, (2, 5):

$$ 2 ∧ 5 = \text{GCD}(2,5) = 1 \in A $$

$$ 2 ∨ 5 = \text{LCM}(2,5) = 10 \notin A $$

In this case, the least upper bound (supremum) does not belong to A.

Therefore, the set (A, |) does not form a lattice.

Example 2

Now consider a different set A, again equipped with the divisibility relation:

$$ ( A = \{1,2,3,6,12 \}, \ | ) $$

The operations remain the same:

• ∧ = GCD (Greatest Common Divisor)
• ∨ = LCM (Least Common Multiple)

In this case, the set does satisfy the conditions for being a lattice.

Every pair of elements in A has both a greatest lower bound and a least upper bound that also belong to A. In other words, the meet and join operations are closed within the set.

(x, y)	GCD	LCM
(1, 2)	1	2
(1, 3)	1	3
(1, 6)	1	6
(1, 12)	1	12
(2, 3)	1	6
(2, 6)	2	6
(2, 12)	2	12
(3, 6)	3	6
(3, 12)	3	12

Example 3

Let’s now consider what happens if we add the element 9 to the previous set:

$$ ( A = \{1,2,3,9,6,12\}, \ | ) $$

With this addition, the structure is no longer a lattice, since the least upper bound of the pair (2, 9) does not exist within the set.

The LCM of 2 and 9 is 18, which is not an element of A.

(x, y)	GCD	LCM
(1, 2)	1	2
(1, 3)	1	3
(1, 9)	1	9
(1, 6)	1	6
(1, 12)	1	12
(2, 3)	1	6
(2, 9)	1	18
(2, 6)	2	6
(2, 12)	2	12
(3, 9)	3	9
(3, 6)	3	6
(3, 12)	3	12

Example 4

Now let’s expand the set further by including the elements 18 and 36:

$$ ( A = \{1,2,3,9,6,12,18,36\}, \ | ) $$

With these additions, the structure once again qualifies as a lattice.

For every pair of elements in A, both the greatest common divisor (meet) and the least common multiple (join) are elements of A. The set is closed under both operations, and all required bounds exist.

(x, y)	GCD	LCM
(1, 2)	1	2
(1, 3)	1	3
(1, 6)	1	6
(1, 9)	1	9
(1, 12)	1	12
(1, 18)	1	18
(1, 36)	1	36
(2, 3)	1	6
(2, 6)	2	6
(2, 9)	1	18
(2, 12)	2	12
(2, 18)	2	18
(2, 36)	2	36
(3, 6)	3	6
(3, 9)	3	9
(3, 12)	3	12
(3, 18)	3	18
(3, 36)	3	36
(6, 9)	3	18
(6, 12)	6	12
(6, 18)	6	18
(6, 36)	6	36
(9, 12)	3	36
(9, 18)	9	18
(9, 36)	9	36
(12, 18)	6	36
(12, 36)	12	36
(18, 36)	18	36

Sub-lattices

A sub-lattice is a subset L′ of a lattice L = (A, ≥) such that, for every pair of elements x, y ∈ L′, both the meet (x ∧ y) and join (x ∨ y) are also elements of L:
$$ \forall x, y \in L' \Rightarrow x ∧ y \in L \quad \text{and} \quad x ∨ y \in L $$

Example

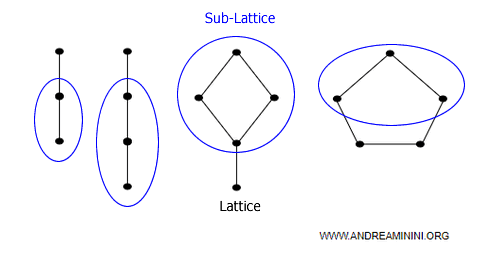
Example

Consider the following three partially ordered sets:

$$ A = \{a, b, c, d, e, f\} $$

$$ B = \{a, c, d, f\} $$

$$ C = \{b, c, d, e\} $$

The corresponding Hasse diagrams are shown below:

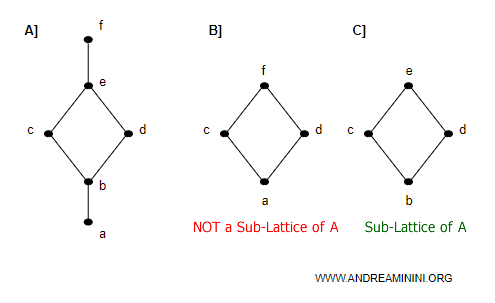
The subset B is not a sub-lattice of A because the greatest lower bound (infimum) of the pair (c, d) in B differs from the infimum of the same pair in A:

$$ \text{In } A: \quad c ∧ d = b $$

$$ \text{In } B: \quad c ∧ d = a $$

Since the meet in B is not consistent with the one in A, B is not a sub-lattice of A.

Note: Although B is not a sub-lattice of A, it is still a lattice in its own right, because every pair of elements in B has both a meet and a join within B itself.

By contrast, subset C is a sub-lattice of A, as all its meets and joins are identical to those in A.

Lattice Homomorphisms and Isomorphisms

A lattice homomorphism is a function A mapping a lattice (L, ≤) to another lattice (L′, ≤) such that, for all x, y ∈ L:
$$ A: L \rightarrow L' $$
$$ A(x ∧ y) = A(x) ∧ A(y) \\ A(x ∨ y) = A(x) ∨ A(y) $$

Example of a lattice homomorphism

Consider the function A defined as squaring each element:

$$ A: x \in L \mapsto x^2 \in L' $$

Suppose the domain lattice is:

$$ L = (\{1, 2, 3, 6, 12\},\ |) $$

Note: As shown in earlier examples, this is a valid lattice under divisibility.

The function A maps each element of L to its square, forming a new set:

$$ L' = (\{1, 4, 9, 36, 144\},\ |) $$

There is a structural correspondence between L and L′:

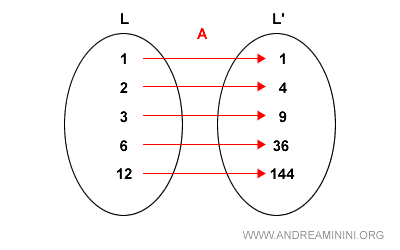
However, the existence of a function between two sets does not guarantee that the image is a lattice. We must explicitly verify that L′ satisfies the lattice properties.

(x, y)	x ∧ y	x ∨ y
(1, 4)	1	4
(1, 9)	1	9
(1, 36)	1	36
(1, 144)	1	144
(4, 9)	1	36
(4, 36)	4	36
(4, 144)	4	144
(9, 36)	9	36
(9, 144)	9	144
(36, 144)	36	144

As we can see, for each pair (x, y) in L′, both x ∧ y and x ∨ y are also elements of L′.

Thus, L′ is indeed a lattice, and the mapping A is a valid lattice homomorphism.

A lattice isomorphism is a bijective homomorphism A such that:
$$ A: L \rightarrow L' \quad \text{and} \quad A^{-1}: L' \rightarrow L $$

Example of a lattice isomorphism

Recall the squaring map defined earlier:

$$ A: x \in L \mapsto x^2 \in L' $$

We already know that both L and L′ are lattices.

The inverse mapping A⁻¹ can be defined by taking the square root:

$$ A^{-1}: x \in L' \mapsto \sqrt{x} \in L $$

Since A is bijective and structure-preserving, it constitutes a lattice isomorphism.

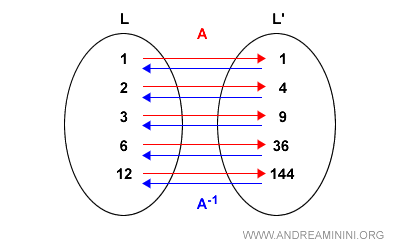
Therefore, A is not only a homomorphism but also an isomorphism.

And so on.