Empty Set

The empty set is a set that contains no elements. It is represented by the symbol Ø or by a pair of empty curly braces { }.

The symbol for the empty set, which is represented as ∅, is read as "empty set" or simply "empty".

A Practical Example of the Empty Set

The set of odd natural numbers divisible by two is empty because no odd natural number is divisible by two

There is only one empty set. The set of odd natural numbers divisible by two is an empty set. Likewise, the set of triangles with four sides is an empty set. In both cases, it is the same empty set even though the membership criteria are different. $$ Ø = \{ \ \ \} $$

The empty set raises intriguing questions about existence in mathematics, as it is an entity that exists without containing anything.

We could describe it as the "nothing" that is actually "something" in the mathematical world.

The Empty Set as an Improper Subset

The empty set is an improper subset of every set.

Proof

To prove this, we begin with a proof by contradiction.

Consider any set A and assume, for contradiction's sake, that the empty set is not a subset of A.

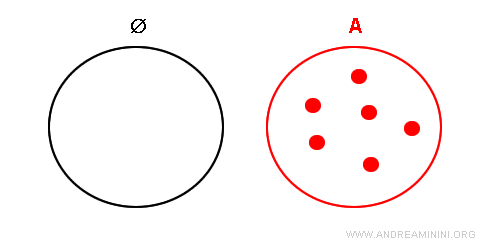
This would imply that there is at least one element in the empty set that is not in A.

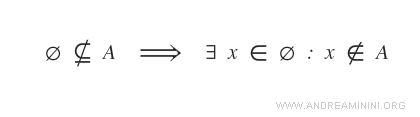
However, this is impossible since the empty set contains no elements.

Once this contradiction is established, the opposite assumption must be true: the empty set is indeed a subset of A.

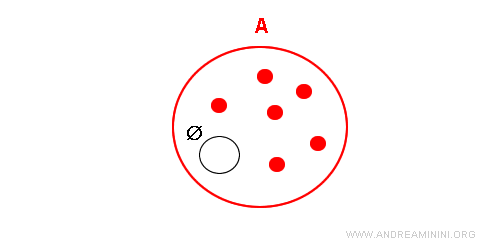
This is why the empty set is considered an improper subset of any set.

Alternative Proof. The union of any set A and any of its subsets B⊆A is always equal to the set itself. $$ A \cup B = A $$ This also happens in the union of the set A and an empty set $$ A \cup Ø = A $$ Therefore, the empty set is also a subset of A.

Key Insights

Here are some notable properties of the empty set:

• There is only one empty set
  Mathematically, there is a singular empty set. Regardless of how or in which context it is used, the empty set is consistently the same entity. This means that the empty set referred to in any mathematical discussion is always the identical mathematical object.

  This uniqueness is critical as it ensures that all the properties associated with the empty set are universal and not dependent on its particular instance or representation. This is why we always refer to it in the singular form as "the empty set," rather than in the plural "empty sets."

• The empty set is a subset of every set
  The empty set is considered an improper subset of every other set, a fundamental and significant concept in mathematics. Hence, it merits a dedicated discussion.

  To grasp this concept, think about the definition of a subset. A set \(A\) is a subset of another set \(B\) if every element of \(A\) is also an element of \(B\). Since the empty set, \(\emptyset\), contains no elements, the requirement that every element of \(\emptyset\) must also be an element of any other set \(B\) is inherently satisfied, no matter what elements \(B\) contains. This means there's no potential for contradiction because the empty set doesn't have any elements to begin with.

• Neutral element in set union
  The union of a set A and the empty set Ø is still set A because the empty set doesn't add any new elements to set A. It’s also known as the identity element of set union. $$ A \cup \emptyset = A $$

  Example. Consider set A = {a, b, c} and the empty set B = { }. The union of the two sets is always set A. $$ A \cup B = \{ a,b,c \} \cup \{ \ \} = \{a,b,c \} = A $$ $$ B \cup A = \{ \ \} \cup \{ a,b,c \} = \{a,b,c \} = A $$

• Neutral element in set difference
  The difference between a set A and the empty set Ø is always set A because there are no elements in common. $$ A - \emptyset = A $$

  Example. The difference between set A = {a, b, c} and the empty set B = { } is still set A. $$ A - B = \{ a,b,c \} - \{ \ \} = \{a,b,c \} = A $$ On the other hand, subtracting set A from the empty set results in the empty set because there are no elements of A to remove. $$ B - A = \emptyset - A = \{ \ \} -  \{ a, b, c \}  = \{ \ \} = B $$

• Absorbing element in set intersection
  The intersection of any set A with the empty set Ø is always the empty set Ø because they have no elements in common. It’s called absorbing because the intersection with any set always results in itself. $$ A \cap \emptyset = \emptyset $$

  Example. The intersection of set A = {a, b, c} and the empty set B = { } is always the empty set B. $$ A \cap B = \{ a,b,c \} \cap \{ \ \} = \{ \ \} = \emptyset $$ $$ B \cap A = \{ \ \}  \cap \{ a,b,c \}  = \{ \ \} = \emptyset $$

• Complement
  The complement of the empty set in a universal set \( U \) is the universal set \( U \) itself.
  

  Example. Consider a universal set U and the empty set Ø, which is an improper subset of any set. Therefore, the complement of the empty set with respect to the universal set U is the universal set U. $$ U \setminus ∅ = U $$

• Cartesian product
  The Cartesian product of any set A with the empty set ∅ is still the empty set ∅ because the empty set has no elements. $$ A \times ∅ = ∅ $$ $$ ∅ \times A = ∅ $$
• Power set
  The power set of the empty set contains only the empty set itself. $$ P(∅) = \{\emptyset \} $$
• The empty set is both open and closed in topology
  The empty set is considered both open and closed in every topological space.
• Is the empty set an improper or proper subset?
  In some mathematics texts, the empty set (∅) is referred to as an improper subset. In others, it's called a proper subset. This difference occurs because the classification depends on the specific definition of "proper subset" being used.

And so on.