The Symmetric Difference of Sets

The symmetric difference between two sets A and B is the set of elements that belong to either one of the sets, but not to both. $$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

This operation helps identify the elements that are unique to each set, excluding those that are shared by both.

Formally, it is expressed as:

$$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Where:

• A\B is the set of elements that belong to A but not to B
• B\A is the set of elements that belong to B but not to A

In other words, the symmetric difference is the union of the differences between the two sets.

It's particularly useful for identifying elements unique to each set.

In Venn diagrams, the symmetric difference between sets is shown as the non-overlapping areas between the two circles representing the sets.

A Practical Example

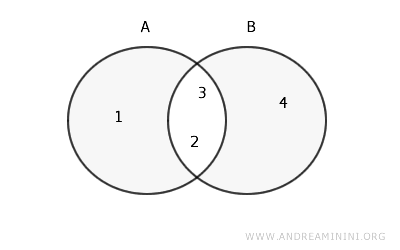
Consider two sets, A and B:

$$ A = \{1, 2, 3\} $$

$$ B = \{2, 3, 4\} $$

The symmetric difference \(A \Delta B\) will consist of the elements that belong to A but not to B, combined with the elements that belong to B but not to A:

$$ A \setminus B = \{1\} $$

$$ B \setminus A = \{4\} $$

So, the symmetric difference between A and B is the set {1, 4}.

$$ A \Delta B = \{1\} \cup \{4\} = \{1, 4\} $$

In terms of Venn diagrams:

Example 2

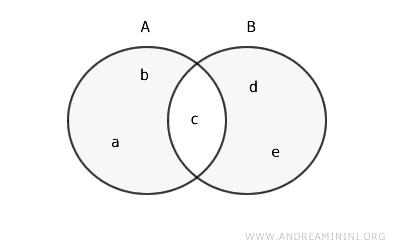
Let's consider another example:

$$ A = \{a, b, c\} $$

$$ B = \{c, d, e\} $$

To calculate the symmetric difference \(A \Delta B\):

$$ A \setminus B = \{a, b\} $$

$$ B \setminus A = \{d, e\} $$

Therefore, the symmetric difference between A and B is the set {a, b, d, e}.

$$ A \Delta B = \{a, b\} \cup \{d, e\} = \{a, b, d, e\} $$

Here's how it's represented with Venn diagrams:

Properties of the Symmetric Difference

The symmetric difference has several interesting properties:

• Commutativity
  The order of the sets does not change the result. \[ A \Delta B = B \Delta A \]
• Associativity
  You can group the sets in different ways without changing the result. \[ A \Delta (B \Delta C) = (A \Delta B) \Delta C \]
• Identity
  The symmetric difference of a set with the empty set is the set itself. \[ A \Delta \emptyset = A \]
• Complementarity
  The symmetric difference of a set with itself is the empty set. \[ A \Delta A = \emptyset \]

And so on.